Science > Physics > Magnetism > Magnetic Dipole Moment of a Magnet
In this article, we shall study the terminology of a bar magnet and the concept of the magnetic dipole moment of a magnet.
Bar Magnet:
A bar magnet is a rectangular parallelepiped body which exhibits magnetic properties. When a bar magnet is suspended in the air such that it is free to rotate about the transverse axis passing through its centre, then it is found that the bar magnet always aligns itself in the north-south direction. The end of the magnet which is pointing towards the geographical north is called north-seeking pole or simply north pole, while the end of the magnet pointing towards the geographical south is called south seeking pole or simply south pole. From the behaviour of a bar magnet, we can say that earth itself is behaving like a magnet. The magnetic north pole of the earth is at geographical south pole while the magnetic south pole of the earth is at the geographical north pole.
A Magnetic Monopole Does Not Exist:
A bar magnet is said to have two poles located at the two ends of the magnet. If we try to break the bar magnet at the centre and separate the poles, new poles are formed at the broken ends. Thus two new magnets are formed each having two opposite poles at their ends. If the magnet is broken down into very small pieces further each piece will be a magnet with two poles. It means it is not possible for us to separate the poles. Thus we can say that a magnetic monopole does not exist.
Fictitious Poles:
It is not possible to separate the two poles (the south pole and the north pole) by breaking the magnet into two parts. Similarly, it is not possible to locate the position of the poles of the magnet. Hence a magnetic dipole is supposed to be made up of two fictitious or imaginary poles. The position of these fictitious poles is found using a compass needle. And it is found that they are not located exactly at the ends of the magnet but slightly inside.
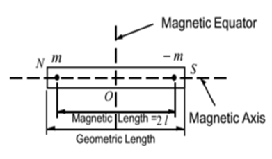
- Geometric Length of magnet: The length of the edge parallel to the magnetic axis is called the geometric length of the bar magnet.
- Magnetic Length of Magnet: The distance between the poles of a bar magnet is called magnetic length.
Magnetic length of bar magnet × 1.2 = Geometric length of the bar magnet.
- Axis of Magnet: The line joining the poles of the bar magnet to called an axis of the magnet.
- Equator of Magnet: The perpendicular drawn to the magnetic axis through the centre of magnet is called the equator of the magnet.
Need of Analogy of Magnetic Circuit with Electric Circuit:
If we try to break the bar magnet at the centre and separate the poles, new poles are formed at the broken ends. It means it is not possible for us to separate the poles and study them individually hence the magnetic circuit is studied in analogy with the electrical circuit. Formulae & concepts are derived from an electrical circuit and by analogy formula for a magnetic circuit is written.
Magnetic Induction at a Point in Magnetic Field:
The magnetic intensity or magnetic induction at any point in the magnetic field is equal to the number of tubes of force passing through the unit area of a small surface element drawn at that point.
B = ∅ / A
Where B = magnetic intensity or intensity of the magnetic field
or magnetic induction.
∅ = Magnetic flux. Its unit as weber (Wb)
A = Area through which magnetic flux pass.
Unit of Magnetic induction B is Wb/m² or tesla (T)
Magnetic Dipole:
A magnetic dipole can be defined as two equal and opposite magnetic poles separated by a finite distance. A magnetic dipole consists of two equal and opposite magnetic charges having pole strength +m & -m separated by finite distance ‘2l’.
Magnetic Dipole Moment:
The magnetic dipole moment is defined as the product of the pole strength and the magnetic length of a magnet.
M = m × 2l
The magnetic dipole moment is a vector quantity. Its direction is from -m to + m i.e. from the south pole to the north pole. SI unit of Magnetic dipole moment is ampere. metre² i.e. Am²
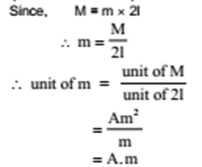
A current-carrying coil behaves like a magnet.
Magnetic dipole moment of current-carrying coil = NiA
Where N = Number of turns of coil
I= Current through the coil
A = Area of the coil
Numerical Problems on Bar Magnet:
Example – 01:
A bar magnet of geometric length 18 cm has pole strength 100 Am. Find the magnetic dipole moment of the bar magnet.
Given: Geometric length of bar magnet = 18 cm = 0.18 m, Pole strength = m = 100 Am
To Find: Magnetic dipole moment = M = ?
Solution:
Magnetic length = (5/6) x Geometric length = (5/6) x 0.18 = 0.15 cm
M = m x magnetic length
∴ M = 100 x 0.15 = 15Am2
Ans: The magnetic dipole moment of bar magnet is 15 Am2.
Example – 02:
A bar magnet of magnetic length 0.1 m has pole strength of 10 Am. What is the dipole moment of this magnet?
Given: Magnetic length of bar magnet = 0.1 m, Pole strength = m = 10 Am
To Find: Magnetic dipole moment = M = ?
Solution:
M = m x magnetic length
∴ M = 10 x 0.1 = 1Am2
Ans: The magnetic dipole moment of bar magnet is 1 Am2.
Example – 03:
A bar magnet of the magnetic moment 5 Am2 has poles 0.2 m apart. Calculate the pole strength.
Given: Magnetic moment = 5 Am2, magnetic length of bar magnet = 0.2 m,
To Find: pole strength = m = ?
Solution:
M = m x magnetic length
∴ m = M/ magnetic length = 5/0.2 = 25 Am
Ans: The pole strength of bar magnet is 25 Am.
Example – 04:
A bar magnet has pole strength 48 Am which are 0.25 m apart. What is the magnetic moment of the magnet?
Given: Magnetic length of bar magnet = 0.25 m, Pole strength = m = 48 Am
To Find: Magnetic dipole moment = M = ?
Solution:
M = m x magnetic length
∴ M = 48 x 0.25 = 12Am2
Ans: The magnetic dipole moment of bar magnet is 12 Am2.
Problems on Magnetic Dipole Moment of Current-Carrying Coil:
Example – 05:
A circular coil of 20 turns and radius 10 cm has a magnetic dipole moment of 3.142 Am2. What is the current flowing through the coil.
Given: Number of turns = n = 20, radius of coil = 10 cm = 0. 1 m, magnetic dipole moment = M = 3.142 Am2.
To Find: Current through the coil = i = ?
Solution:
M = n I A
∴ i = M/nA = M/ (n x π r2 )
∴ i = 3.142/ (20 x 3.142 x (0.1)2 ) = 5 A
Ans: The current through the coil is 5 A.
Example – 06:
A circular coil of 50 turns and 10 cm radius carries a current of 2 A. Find the magnetic moment of the coil.
Given: Number of turns = n = 50, radius of coil = 10 cm = 0. 1 m, Current through coil = i = 2 A.
To Find: Magnetic dipole moment = M = ?
Solution:
M = n i A = n i (π r2)
∴ M = 50 x 2 x 3.142 x (0.1)2 = 3.142 Am2
Ans: The magnetic dipole moment is 3.142 Am2.
Example – 07:
A circular coil has 1000 turns each of area 2 m2. If a current of 3 mA flows through the coil, find the magnetic moment of the coil.
Given: Number of turns = n = 1000, Area of coil = A = 2 m2, Current through coil = i = 3 mA = 3 x 10-3 A
To Find: Magnetic dipole moment = M = ?
Solution:
M = n i A
∴ M = 1000 x 3 x 10-3 x 2 = 6Am2
Ans: The magnetic dipole moment is 6 Am2.
Example – 08:
A rectangular coil of length 8 cm and breadth 5 cm has 200 turns of insulated wire. Find the magnetic dipole moment of the coil. When a current of 2 A flows through it.
Given: Number of turns = n = 200, Area of coil = A = 8 cm x 5 cm = 40 cm2 = 40 x 10-4 m2, Current through coil = i = 2 A
To Find: Magnetic dipole moment = M = ?
Solution:
M = n i A
∴ M = 200 x 40 x 10-4 x 2 = 1.6Am2
Ans: The magnetic dipole moment is 1.6 Am2.
Example – 09:
A steel wire of length ‘l‘ has a magnetic moment M. If the wire is bent in a semicircular arc, what would its moment be?
Solution:
Let m be the pole strength
Now, M = m x magnetic length
∴ m = M/l
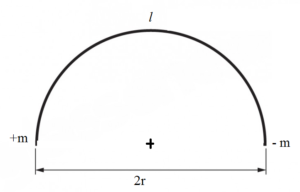
Curved length of semicircle = half circumference
∴ l = π r
∴ r = l /π
Now new magnetic dipole moment
M = m x new magnetic length
∴ M = (M/l)x 2r = (M/l)x 2 x (l /π) = 2M/π
Ans: New magnetic moment is 2M/π
Previous Subject: Types of Magnetic Materials