Science > Physics > Magnetism > Magnetization and Magnetic Intensity
In this article, we shall study the origin of magnetism, magnetic intensity, magnetization, and magnetic susceptibility.
Magnetic Field Due to Current-Carrying Coil:
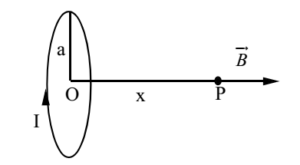
The magnetic induction at a point on the axis at a distance of ‘x’ from the centre of a circular coil of radius ‘a’ is given by
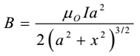
It is directed along the axis of the coil and away from it and perpendicular to the plane of the coil. For x >>a, we can neglect a² from denominator in the expression.

This is an expression for magnetic induction due to current carrying loop
Now, the electric intensity due to electric dipole on its axis is given by

From the two equations (3) and (4) we can say that the magnetic dipole moment is analogous to electrostatic dipole moment P and the magnetic field is analogous to the electric field. Thus the planar current loop is analogous to a magnetic dipole. i.e. current-carrying loop produces a magnetic field and behaves like a magnetic dipole.
Dipole Moment of Revolving Electron:

The origin of magnetism in substances can be explained by considering the circular motion of electrons. The negatively charged electrons in atoms move in circular orbits around the positively charged nucleus which are equivalent to a circular coil carrying current.
The period of revolution of electron

The direction of this magnetic moment is into the plane of the paper.
If me is the mass of the electron, multiplying and dividing numerator and denominator of R.H.S.

Lo is the angular momentum of the electron which is coming out of the plane of the paper. The quantities e, me are constant, hence the magnetic dipole moment of the electron is directly proportional to its angular momentum. The angular momentum of electron and magnetic dipole moment are opposite to each other. In vector form

The ratio of magnetic dipole moment to the angular momentum of the revolving electron is constant and is called the gyromagnetic ratio.

Gyromagnetic ratio is also called the magnetogyric ratio.
The orbital motion of electrons gives rise to an orbital magnetic moment. In addition, the electrons spin about its own axis constituting a spin magnetic moment. The resultant magnetic moment of an atom is the vector sum of the orbital and spin magnetic moment.
Origin of Magnetism on the Basis of Circulating Charges:
The origin of magnetism in substances can be explained by considering the circular motion of electrons. The electrons in atoms move in circular orbits around the nucleus which are equivalent to a circular coil carrying current.
The orbital motion of electrons gives rise to an orbital magnetic moment. In addition, the electrons spin about its own axis constituting a spin magnetic moment. The resultant magnetic moment of an atom is the vector sum of the orbital and spin magnetic moment. These small magnets are called elementary or atomic magnets. When the material is not magnetized, these elementary magnets form closed chains thereby annualizing each other’s effect. When the material is magnetized, these elementary magnets are aligned in the same direction.

On the basis of magnetic properties, substances are classified into three groups namely diamagnetic, paramagnetic and ferromagnetic.
The Atomic theory of magnetism explains following facts.
- Single poles cannot exist. Poles always exist in a pair.
- The magnetic poles of a magnet are of equal strength.
- When a magnet is heated, the thermal energy of atomic magnet increases. Due to which they again form closed chain and
magnetism is lost.
Magnetization of Ferromagnetic Material using Rowland Ring (Toroid With Iron Core):
The magnetization of a ferromagnetic material such as iron can be studied with an arrangement called Toroid with an iron core.

Let the toroid have ‘n’ number of turns per unit length and ‘I’ be the current through it. The magnitude of magnetic field inside the coil when iron core is not present is given by
B0 = μ0 n I
When an iron core is present in the toroid, the magnetic field increases, which is given by
B = B0 + BM ……… (1)
Where BM is magnetic field contributed by the iron core.
It is found that BM is directly proportional to magnetization of iron and is given by
BM = μ0 Mz ……. (2)
The strength of magnetic field at a point can be given in terms of vector quantity called magnetic intensity (H).
Thus B0 = μ0 H ……… (3)
Where, H = nI. Unit of magnetic intensity is A/m and its dimensions are [L-1M0T0I1].
Substituting values of equations (2) and (3) in (1)
B = μ0 H + μ0 Mz
B = μ0 (H + Mz ) ………….. (4)
Magnetization can be expressed in terms of magnetic intensity as
Mz = χ H
Where χ (chi) is called the magnetic susceptibility.
Substituting in equation (4)
B = μ0 (H + χ H)
∴ B = μ0 (1 + χ ) H
The quantity (1 + χ ) is called relative magnetic permeability and is denoted by μr. It is a dimensionless quantity
∴ B = μ0 μr H = μ H
Note:
μr is called relative magnetic permeability of the substance. μis called absolute magnetic permeability of the substance. μ0 is called magnetic permeability of free space.
Terminology:
Magnetization:
The net magnetic dipole moment per unit volume is called as the magnetization of a sample. It is denoted by Mz. It is a vector quantity. S.I. unit of magnetization is A/m and its dimensions are [AL-1]. By definition, magnetization.

Magnetic Intensity:
Magnetic intensity is a quantity used in describing the magnetic phenomenon in terms of their magnetic fields. The strength of magnetic field at a point can be given in terms of vector quantity called magnetic intensity (H). S.I. unit of magnetization is A/m and its dimensions are [AL-1]. By definition, magnetic intensity

Magnetic susceptibility:
The ratio of the intensity of magnetization to magnetic intensity is called magnetic susceptibility. Magnetic susceptibility is dimensionless and unitless quantity. By definition,

Magnetic Permeability:
The ratio of the magnitude of the total field inside the material to that of the magnetic intensity of the magnetizing field is called magnetic permeability. S.I. unit of magnetic permeability is H/m. Its dimensions are [L1M1T-2I-2]. By definition
μ = B / H
Relative Permeability:
The ratio of the magnitude of the total field inside the material to that of magnetizing field is called relative permeability. Relative permeability is dimensionless and unitless quantity. By definition,
μr = B / B0
Curie’s Law of Magnetization:
The magnetization of a paramagnetic sample is directly proportional to the external magnetic field and inversely proportional to the absolute temperature.
