Numerical Problems on Magnetic Susceptibility

Science > Physics > Magnetism > Numerical Problems on Magnetic Susceptibility

In this article, we shall study problems to calculate magnetization, magnetic susceptibility, magnetic permeability, etc.

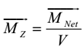
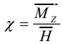
μ = B / H

μ_r  = B / B₀

Example – 01:

Find the magnetization of the bar magnet of length 10 cm and cross-sectional area 3 cm². The magnetic moment of the magnet is 1 Am².

Given: Length of magnet = l = 10 cm, cross-sectional area = A = 3 cm², Magnetic moment = M =  1 Am².

To Find: Magnetization = M_Z = ?

Solution:

Volume of bar magnet = V = length x cross-sectional area = 10 x 3 = 30 cm³ = 30 x 10^-6 m³.

M_Z = M/V = 1/ (30 x 10^-6) = 3.33 x 10⁴ A/m.

Ans: Magnetization of the bar magnet is 3.33 x 10⁴ A/m.2

Example – 02:

Find the magnetization of the bar magnet of length 5 cm and cross-sectional area 2 cm². The magnetic moment of the magnet is 1 Am².

Given: Length of magnet = l = 5 cm, cross-sectional area = A = 2 cm², Magnetic moment = M =  1 Am².

To Find: Magnetization = M_Z = ?

Solution:

Volume of bar magnet = V = length x cross-sectional area = 5 x 2 = 10 cm³ = 10 x 10^-6 m².

M_Z = M/V = 1/ (10 x 10^-6) = 1 x 10⁵ A/m.

Ans: Magnetization of the bar magnet is 1 x 10⁵ A/m.

Example – 03:

Find the magnetization of bar magnet of mass 180 g, the density of material 8 g/cm³ and the magnetic moment 3.5 Am².

Given: Mass of magnet = m = 180 g, Density of material of magnet = 8 g/cm³, Magnetic moment = M =  3.5 Am².

To Find: Magnetization = M_Z = ?

Solution:

Density = Mass / Volume

∴  Volume = Mass/density = 180/8 = 22.5 cm³ = 22.5 x 10^-6 m².

M_Z = M/V = 3.5/ (22.5 x 10^-6) = 1.56 x 10⁵ A/m.

Ans: Magnetization of the bar magnet is 1.56 x 10⁵ A/m.

Example – 04:

A bar magnet made of steel has a magnetic moment of 2.5 Am² and a mass of 6.6 x 10^-3 kg. If the density of steel is 7.9 x 10³ kg/m³, find the intensity of the magnetization of the magnet.

Given: Mass of magnet = m = 6.6 x 10^-3 kg, Density of material of magnet = 7.9 x 10³  kg/m³, Magnetic moment = M =  2.5 Am².

To Find: Magnetization = M_Z = ?

Solution:

Density = Mass / Volume

∴  Volume = Mass/density = (6.6 x 10^-3)/(7.9 x 10³) = 8.354 x 10^-7 m².

M_Z = M/V = 2.5/ (8.354 x 10^-7) = 3.0 x 10⁶ A/m.

Ans: Magnetization of the bar magnet is 3.0 x 10⁶ A/m.

Example – 05:

Magnetic field and magnetic intensity are respectively 1.8 T and 1000 A/m. Find relative permeability and susceptibility.

Given: Magnetic field = B = 1.8 T, magnetic intensity = H = 1000 A/m, μ_o = 4π x 10^-7 Wb/Am.

To Find: Relative permeability = μ_r = ?, susceptibility = χ = ?

Solution:

μ_r = B/(μ_oH) = 1.8/(4π x 10^-7 x 1000) =1.8/(4 x 3.142 x 10^-4) = 1.432 x 10³  = 1432

We have μ_r = 1 + χ

∴  χ = μ_r – 1 =  1432 – 1 = 1431

Ans: Relative permeability is 1432 and susceptibility is 1431.

Example – 06:

Magnetic field and magnetic intensity are respectively 1.6 T and 1000 A/m. Find relative permeability and susceptibility.

Given: Magnetic field = B = 1.6 T, magnetic intensity = H = 1000 A/m, μ_o = 4π x 10^-7 Wb/Am.

To Find: Relative permeability = μ_r = ?, susceptibility = χ = ?

Solution:

μ_r = B/(μ_oH) = 1.6/(4π x 10^-7 x 1000) =1.6/(4 x 3.142 x 10^-4) = 1.273 x 10³  = 1273

We have μ_r = 1 + χ

∴  χ = μ_r – 1 =  1273 – 1 = 1272

Ans: Relative permeability is 1273 and susceptibility is 1272.

Example – 07:

Magnetic field and magnetic intensity are respectively 1.3 T and 900 A/m. Find permeability, relative permeability, and susceptibility.

Given: Magnetic field = B = 1.3 T, magnetic intensity = H = 900 A/m, μ_o = 4π x 10^-7 Wb/Am.

To Find: permeability = μ = ?, relative permeability = μ_r = ?, susceptibility = χ = ?

Solution:

μ = B/H = 1./900 = 1.44 x 10^-3

μ_r = B/(μ_oH) = 1.3/(4π x 10^-7 x 900) =1.3/(4 x 3.142 x 10^-7 x 900) = 1.149 x 10³  = 1149

We have μ_r = 1 + χ

∴  χ = μ_r – 1 =  1149 – 1 = 1148

Ans: Permeability is 1.44 x 10^-3, relative permeability is 1149 and susceptibility is 1148.

Example – 08:

The susceptibility of annealed iron at saturation is 5500. Find the permeability of annealed iron at saturation.

Given: susceptibility = χ = 5500,  μ_o = 4π x 10^-7 Wb/Am.

To Find: permeability at saturation = μ = ?

Solution:

μ = μ_o ( 1 + χ)

∴  μ = 4π x 10^-7  ( 1 + 5500) =  4 x 3.142 x 10^-7 x 5501 = 6.9 x 10^-3 H/m.

Ans: Permeability at saturation is  6.9 x 10^-3 H/m.

Example – 09:

The susceptibility of magnetic material at saturation is 4000. Find its permeability at saturation.

Given: susceptibility = χ = 4000,  μ_o = 4π x 10^-7 Wb/Am.

To Find: permeability at saturation = μ = ?

Solution:

μ = μ_o ( 1 + χ)

∴  μ = 4π x 10^-7  ( 1 + 4000) =  4 x 3.142 x 10^-7 x 4001 = 5.028 x 10^-3 H/m.

Ans: Permeability at saturation is  5.028 x 10^-3 H/m.

Example – 10:

An iron rod is subjected to a magnetizing field of 1200 A/m. The susceptibility of iron is 599. Find the permeability and the magnetic flux per unit area produced.

Given: Magnetizing field = H = 1200 A/m, susceptibility = χ = 599,  μ_o = 4π x 10^-7 Wb/Am.

To Find: permeability = μ = ?, Magnetic flux per unit area = B = ?

Solution:

μ = μ_o ( 1 + χ)

∴  μ = 4π x 10^-7  ( 1 + 599) =  4 x 3.142 x 10^-7 x 600 = 7.536 x 10^-4 H/m.

Now μ = B/H

∴ B = μ H =  7.536 x 10^-4 x 1200 =  0.904T

Ans: Permeability is  7.536 x 10^-4 H/m and magnetic flux per unit area = 0.904 T

Example – 11:

The susceptibility of magnesium at 300 K is 1.2 x 10^-5. At what temperature will the susceptibility increases to 1.8 x 10^-5.

Given: Initial temperature = T₁ = 300K, Initial susceptibility = χ₁ = 1.2 x 10^-5, Final susceptibility = χ₂ = 1.8 x 10^-5.

To Find: Final temperature = T₂ = ?

We have χ ∝ 1/T

∴  χ₁/χ₂ = T₂/T₁

∴  T₂ = (χ₁/χ₂) x T₁

∴  T₂ = (1.2 x 10^-5/1.8 x 10^-5) x 300 = = (2/3) x 300 = 200 K

Ans: At temperature 200 K, magnetic susceptibility increases to 1.8 x 10^-5.

Example – 12:

The susceptibility of magnesium at 400 K is 1.5 x 10^-5. At what temperature will the susceptibility increases to 1.8 x 10^-5.

Given: Initial temperature = T₁ = 400K, Initial susceptibility = χ₁ = 1.5 x 10^-5, Final susceptibility = χ₂ = 1.8 x 10^-5.

To Find: Final temperature = T₂ = ?

We have χ ∝ 1/T

∴  χ₁/χ₂ = T₂/T₁

∴  T₂ = (χ₁/χ₂) x T₁

∴  T₂ = (1.5 x 10^-5/1.8 x 10^-5) x 400 = = (5/6) x 400 = 333.33 K

Ans: At temperature 333.33 K susceptibility increases to 1.8 x 10^-5.

Example – 13:

The susceptibility of magnetic material at 250 K is 1.44 x 10^-5. At what will the value of susceptibility at 300 K.

Given: Initial temperature = T₁ = 250 K, Initial susceptibility = χ₁ = 1.44 x 10^-5,  1.8 x 10^-5, Final temperature = T₂ = 300 K

To Find: Final susceptibility = χ₂ = ?

Solution:

We have χ ∝ 1/T

∴  χ₁/χ₂ = T₂/T₁

∴  χ₂ = (T₁/T₂) x χ₁

∴  χ₂ = (250/300) x 1.44 x 10^-5 = = (5/6) x 1.44 x 10^-5 = 1.2 x 10^-5

Ans: At temperature 300 K magnetic susceptibility is 1.2 x 10^-5.

Science > Physics > Magnetism > Numerical Problems on Magnetic Susceptibility