Shear Stress, Shear Strain, and Modulus of Rigidity

Science > Physics > Elasticity > Shear Stress, Shear Strain, and Modulus of Rigidity

In this article, we shall study the concept of shear stress, shear strain, and modulus of rigidity.

Shear Stress:

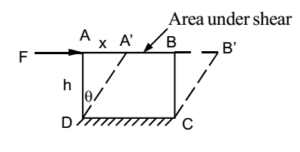
When the deforming forces are such that there is a change in the shape of the body, then the stress produced is called shearing stress. Shear stress is also called as tangential stress.

Mathematically,

Shear stress = Shearing force (F) / Area under shear

Its S.I. unit of stress is N m^-2 or Pa (pascal) and its dimensions are [L^-1M¹T^-2].

Shear Strain:

When the deforming forces are such that there is a change in the shape of the body, then the strain produced in the body is called shear strain.

Shearing strain is defined as the ratio of relative displacement of any layer to its perpendicular distance from the fixed layer.

Mathematically,

tan θ = x/h

Modulus of Rigidity:

Within the elastic limit, the ratio of the shear stress to the corresponding shear strain in the body is always constant, which is called modulus of rigidity.

It is denoted by the letter ‘η’. Its S.I. unit of stress is N m^-2 or Pa (pascal) and its dimensions are [L^-1M¹T^-2].

Consider a rigid body as shown in the figure which is fixed along the surface CD.  Let it be acted upon by tangential force F along surface AB as shown. Let lateral surface AD get deflected through angle θ as shown. The tangential force F per unit area of surface AB is called shear stress.

Characteristics of Modulus of Rigidity or Shear Modulus:

• Within the elastic limit, it is the ratio of shear stress to shear strain
• It is associated with the change in the shape of a body.
• It exists in solids only.
• It describes an object’s tendency to shear
• The shear modulus of a material of a body is given by

Characteristics of Moduli of Elasticity:

• Modulus of elasticity is the property of the material of a body and is independent of the stress and strain on the body.
• a material is said to be elastic if it has a greater value of modulus of elasticity.
• The modulus of elasticity for rigid bodies is infinity.
• Young’s modulus is the property of solids only. While bulk modulus exists for all the three states of matter.
• Gases possess two bulk moduli of elasticity. (i) Isothermal bulk modulus K_iso = P and (ii) Adiabatic bulk modulus K_adia = γP
• The elasticity of a substance decreases with the increase in the temperature.

Distinguishing Between Young’s Modulus, Bulk Modulus and Modulus of Rigidity:

Young’s Modulus of Elasticity	Bulk Modulus of Elasticity	Modulus of Rigidity
Within the elastic limit, it is the ratio of longitudinal stress to longitudinal strain	Within the elastic limit, it is the ratio of volumetric stress to volumetric strain	Within theelastic limit, it is the ratio of shear stress to shear strain
It is associated with the change in the length of a body.	It is associated with the change in the volume of a body.	It is associated with the change in the shape of a body.
It exists in solid material bodies	It exists in solids, liquids, and gases.	It exists in solids only.
It is a measure of the stiffness of a solid material	It determines how much the body will compress under a given amount of external pressure.	It describes an object’s tendency to shear
Young’s modulus of the material of a wire is given by	The bulk modulus of the material of a body is given by	Shear modulus of the material of a body is given by

Relation Between the Moduli of Elasticity:

Numerical Problems:

Example – 1:

The area of the upper face of a rectangular block is 0.5 m x 0.5 m and the lower face is fixed. The height of the block is 1 cm. a shearing force applied to the top face produces a displacement of 0.015 mm. Find the strain, stress and the shearing force. Modulus of rigidity = η = 4.5 × 10¹⁰ N/m².

Given: Area under shear = A = 0.5 m x 0.5 m = 0.25 m², Height of the block = h = 1 cm = 1 × 10^-2 m, Displacement of top face = x = 0.015 mm = 0.015 × 10^-3 m = 1.5 × 10^-5 m, Modulus of rigidity = η = 4.5 × 10¹⁰ N/m².

Solution:

To Find: Shear strain =? Shear stress =? Shearing force = F =?

Shear strain = tanθ = x/h = (1.5 × 10^-5) / (1 × 10^-2) = 1.5 × 10^-3
Modulus of rigidity = η = Shear stress / Shear strain
∴ Shear stress = η × Shear strain = 4.5 × 10¹⁰ × 1.5 × 10^-3
∴ Shear stress = 6.75 × 10⁷ N/m².
Shear stress = F/A
∴ F = Shear stress × Area
∴ F = 6.75 × 10⁷ × 0.25
∴ F = 1.69 × 10⁷ N
Ans: Shear strain = 1.5 × 10^-3, Shear stress = 6.75 × 10⁷ N/m²,

Shearing force = 1.69 × 10⁷ N.

Example – 2:

A metallic cube of side 5 cm, has its lower surface fixed rigidly. When a tangential force of 10⁴ kg. wt. is applied to the upper surface, it is displaced through 0.03 mm. Calculate (1) the shearing stress (2) the shearing strain and (3) the modulus of rigidity of the metal.

Given: Area under shear = A = 5 cm x 5 cm = 25 cm² = 25 × 10^-4 m², Height of the block = h = 5 cm = 5 × 10^-2 m, Displacement of top face = x = 0.03 mm = 0.03 × 10^-3 m =  3 × 10^-5 m, Shearing force  = 10⁴ kg-wt = 10⁴ × 9.8 N.

To Find: Shear strain =? Shear stress =? Modulus of rigidity = η =?

Solution:

Shear stress =  F/A
∴   Shear stress =  (10⁴ × 9.8)/( 25 × 10^-4)
∴   Shear stress = 3.92 × 10⁷ N
Shear strain = tanθ = x/h = (3 × 10^-5 ) / (5 × 10^-2 ) = 6 × 10^-4
Modulus of rigidity = η = Shear stress / Shear strain
η = (3.92 × 10⁷) / (6 × 10^-4) = 6.53 × 10¹⁰   N/m²
Ans: Shear stress = 3.92 × 10⁷ N Shear strain = 6 × 10^-4,

Modulus of rigidity = 6.53 × 10¹⁰   N/m²

Example – 3:

A 5 cm cube of substance has its upper face displaced by 0.65 cm by a tangential force of 0.25 N. Calculate the modulus of rigidity of the substance.

Given: Area under shear = A = 5 cm x 5 cm = 25 cm² = 25 × 10^-4 m², Height of the block = h = 5 cm = 5 × 10^-2 m, Displacement of top face = x = 0.65 cm = 0.65 × 10^-2 m = 6.5 × 10^-3 m, Shearing force  = 0.25 N.

To Find: Modulus of rigidity = η =?

Solution:

Modulus of rigidity = η = Fh/Ax
∴ η = (0.25 × 5 × 10^-2) / (25 × 10^-4 × 6.5 × 10^-3)
∴  η =769 N/m²
Ans: Modulus of rigidity = 769N/m²

Example – 4:

A tangential force of 2100 N is applied on a surface area 3 × 10^-6 m² which is 0.1 m from a fixed face of a block of material. The force produces a shift of 7 mm of the upper surface with respect to the bottom. Calculate the modulus of rigidity of the material.

Given: Area under shear = A = 3 × 10^-6 m², Height of the block = h = 0.1 m, Displacement of top face = x = 7 mm = 7 × 10^-3 m, Shearing force = 2100 N.

To Find: Modulus of rigidity = η =?

Solution:

Modulus of rigidity = γ = Fh/Ax
∴ η = (2100 × 0.1) / (3 × 10^-6  × 7 × 10^-3)
∴  η =10¹⁰ N/m²
Ans: Modulus of rigidity = 10¹⁰ N/m²

Example – 5:

A metal plate has an area of face 1m x 1m and thickness of 1 cm. One face of a larger area is fixed and a tangential force is applied to the opposite face. The displacement of the edge produced thereby is 0.005 cm. Find the shearing stress, strain and magnitude of the tangential force applied. Modulus of rigidity of metal is ϒ = 8.4 × 10¹⁰ N/m²

Given: Area under shear = A = 1 m x 1 cm = 1 m², Thickness of plate = h = 1 cm = 1 × 10^-2 m, Displacement of top face = x = 0.005 cm = 0.005 × 10^-2 m =  5 × 10^-5 m, Modulus of rigidity = η = 8.4 × 10¹⁰ N/m²

To Find: Shear strain =? Shear stress =? Shearing force = F =?

Solution:

Shear strain = tanθ = x/h = (5 × 10^-5) / (1 × 10^-2) = 5 × 10^-3
Modulus of rigidity = η = Shear stress / Shear strain
∴ Shear stress = η × Shear strain = 8.4 × 10¹⁰ × 5 × 10^-3
∴ Shear stress = 4.2 × 10⁸ N/m².
Shear stress = F/A
∴ F = Shear stress × Area
∴ F = 4.2 × 10⁸ ×1
∴ F = 4.2 × 10⁸ N
Ans: Shear strain = 5 × 10^-3, Shear stress = 4.2 × 10⁸ N/m²,

Shearing force = 4.2 × 10⁸  N.

Example – 6:

A metal plate has an area of face 1m x 1m and thickness of 5 cm. One face of a larger area is fixed and a tangential force is applied to the opposite face. The displacement of the edge produced thereby is 0.005 cm. Find the shearing stress and shear strain. Modulus of rigidity of metal is η = 4.2 × 10⁶ N/m²

Given: Area under shear = A = 1 m x 1 cm = 1 m², Thickness of plate = h = 5 cm = 5 × 10^-2 m, Displacement of top face = x = 0.005 cm = 0.005 × 10^-2 m = 5 × 10^-5 m, Modulus of rigidity = η = 4.2 × 10⁶ N/m²

To Find: Shear strain =? Shear stress =? Shearing force = F =?

Solution:

Shear strain = tanθ = x/h = (5 × 10^-5) / (5 × 10^-2) = 10^-3
Modulus of rigidity = η = Shear stress / Shear strain
∴  Shear stress = η × Shear strain =  4.2 × 10⁶  × 10^-3
∴  Shear stress = 4.2 × 10³ N/m².
Ans: Shear strain = 10^-3, Shear stress = 4.2 × 10³ N/m².

Example – 7:

A copper metal cube has each side of length 1m. The bottom edge of a cube is fixed and a tangential force of 4.2 × 10⁸ N is applied to the top surface. Calculate the lateral displacement of the surface, if the modulus of rigidity of copper is 14 × 10¹⁰ N/m².

Given: Area under shear = A = 1 m x 1 cm = 1 m², Height of cube = h =1 m, Modulus of rigidity = η = 14 × 10¹⁰ N/m², Shearing force = F = 4.2 × 10⁸ N

To Find: Displacement of top face = x =?

Solution:

Modulus of rigidity = η = Fh/Ax
∴  x = Fh/Aη
∴  x =  ( 4.2 × 10⁸ × 1)/(1 ×14 × 10¹⁰ )
∴  x =  ( 4.2 × 10⁸ × 1)/(1 ×14 × 10¹⁰ )
∴  x = 3 × 10^-3 m = 3mm
Ans: Displacement of top face is3mm

Example – 8:

The frame of a brass plate of an outer door design has area 1.60 m² and thickness 1cm. The brass plate experiences a shear force due to the earthquake.  How large parallel force must be exerted on each of the edges if the lateral displacement is 0.32 mm. Modulus of rigidity for brass is 3.5 × 10¹⁰ N/m².

Given: Area under shear = A = 1.60 m², Thickness = h =1 cm =1 × 10^-2 m, Modulus of rigidity = η = 3.5 × 10¹⁰ N/m², Displacement of top face = x = 0.32 mm = 0.32 × 10^-3 m =3.2 × 10^-4 m

To Find: Shearing force = F =?

Solution:

Modulus of rigidity = η = Fh/Ax
∴ F = Aηx /h
∴ x = ( 1.60 × 3.5 × 10¹⁰ × 3.2 × 10^-4)/(1 × 10^-2 )
∴  x = 1.792 × 10⁹ N
Ans: Shearing force is 1.792 × 10⁹ N

Previous Topic: Volumetric Stress, Volumetric Strain, and Bulk Modulus

Next Topic: Concept of Strain Energy and Numerical Problems

Science > Physics > Elasticity > Shear Stress, Shear Strain, and Modulus of Rigidity