Motion in a Vertical Circle

Science > Physics > Circular Motion > Motion in Vertical Circle

When studying the motion of a body in a vertical circle we have to consider the effect of gravity. Due to the influence of the earth’s gravitational field, the magnitudes of the velocity of the body and tension in the string change continuously. It is maximum at the lowest point and minimum at the highest point. Hence the motion in vertical circle is not uniform circular motion.

The Expression for Velocity of Body Moving in a Vertical Circle:

Consider a small body of mass ‘m’ attached to one end of a string and whirled in a vertical circle of radius ‘r’. In this case, the acceleration of the body increases as it goes down the vertical circle and decreases when goes up the vertical circle. Hence the speed of the body changes continuously. It is maximum at the bottommost position and minimum at the uppermost position of the vertical circle. Hence the motion of the body is not uniform circular motion. Irrespective of the position of the particle on the circle, the weight ‘mg’ always acts vertically downward.

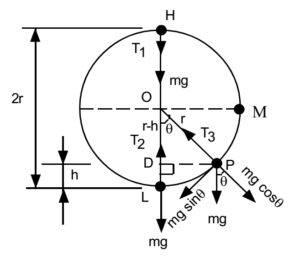
Let ‘v’ be the velocity of the body at any point P on the vertical circle. Let L be the lowest point of the vertical circle. Let ‘h’ be the height of point P above point L. let ‘u’ be the velocity of the body at L. By the law of conservation of energy

Energy at point P = Energy at point L

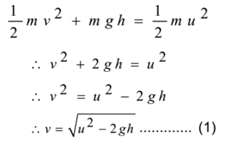
This is an expression for the velocity of a particle at any point performing a circular motion in a vertical circle.

The Expression for Tension in the String in Motion of Body in Vertical Circle:

Consider the centripetal force at point P

Substituting in equation (2)

This is the expression for the tension in the string.

Special Cases:

Case – I: When the body is at the lowermost position i.e. body is at L) (h = 0)

Case – II: When the body is at the uppermost position i.e. body is at H (h = 2r)

Case – III: When the string is horizontal i.e. body is at M (h = r)

Relation Between Tension at the Highest point and at the Lowest Point:

Thus the difference in tensions at the two positions

Thus the tension in the string at the lowest point L is greater than the tension at the highest point H by six times the weight of the body.

Minimum Velocity of Body at Different Positions When Looping a Loop:

Lowest Point L (h = 0):

This is the minimum velocity of the body required so that the body looping a loop i.e. to go round the circle once completely.

This is the minimum velocity at the lowest point of the vertical circle required for a body looping a loop.

Highest Point H (h = 2r):

This is the minimum velocity at the highest point of the vertical circle required for a body looping a loop.

When String is Horizontal  (h = r):

This is the minimum velocity when the string is horizontal at the point M of the vertical circle required for a body looping a loop.

If the velocity ‘v’ of the body is such that, v ≤ √2gr, then the body oscillates about point L, the lowest point of the vertical circle.

If the velocity ‘v’ of the body is such that √2gr < v < √5gr , then the body leaves the circular path and acts like a projectile. It will leave circular motion between M and H.

Energy of Body Moving in a Vertical Circle:

The energy of the body has two components a) kinetic energy (E_K) and b) potential energy (E_P). Sum of the two energies is total energy (E_T)

At Lowest Point L:

At Highest Point H:

When String is Horizontal:

Study Above Proof in Video Lecture

Notes:

Kinetic energy is maximum at the lowest point of the circular path and minimum at the highest point of the circular path. Total energy is conserved.

Uniform Circular Motion in a Vertical Circle

Let us consider a body performing U.C.M. in a vertical circle with constant speed ‘v’. Then,

Tension in String and Acceleration of Particle:

At the Highest Point:

a=v²/r

The direction of tension acceleration is vertically downward

At the Lowest Point:

a=v²/r

The direction of tension acceleration is vertically upward

When String is Horizontal:

a=v²/r

The direction of tension acceleration is horizontal and towards the centre.

At Any Position:

Note:

The difference in tension at the lowest point and the highest point is = 2mg

Numerical Problems on Motion in Vertical Circle:

Example – 01:

A stone weighing 1 kg is whirled in a vertical circle at the end of a rope of length 0.5 m. Find the velocity of a stone at a) lowest position b) midway when the string is horizontal c) topmost position to just complete the circle.

Given: Radius of circular path = r = 0.5 m, Mass of the body = m = 1 kg, g = 9.8 m/s²,

To find: velocity at lowest point = v_L =? velocity when string is horizontal = v_M = ?, velocity at topmost point = v_H = ?.

Solution:  

Ans: Velocity of stone at the lowermost point = 4.95 m/s, The velocity of stone when the string is horizontal = 3.83 m/s, The velocity of stone at the topmost point = 2.21 m/s

Example – 02:

A stone weighing 1 kg is whirled in a vertical circle at the end of a rope of length 0.5 m. Find the tension in the string at a) lowest position b) midway when the string is horizontal c) topmost position to just complete the circle.

Given: Radius of circle = r = 0.5 m, mass of the body = m = 1 kg, g = 9.8 m/s².

To find: Tension at lowest point = T_L =? Tension when string is horizontal = T_M = ?, Tension at topmost point = T_H = ?.

Solution:

Ans: Tension at the lowermost point = 58.8 N, Tension when string is horizontal  = 29.4 N, Tension at topmost point = 0 N

Example – 03:

A stone weighing 50 g is whirled in a vertical circle at the end of a rope of length 1.8 m. Find the tension in the string at a) lowest position b) midway when the string is horizontal c) topmost position to just complete the circle.

Given: Radius of circle = r =1.8 m, mass of the body = m = 50 g =0.050 kg, g = 9.8 m/s²,

To find: Tension at lowest point = T_L =? Tension when string is horizontal = T_M = ?, Tension at topmost point = T_H = ?,

Solution:

Ans: Tension at lowermost point = 2.94 N, Tension when string is horizontal  = 0 N, Tension at topmost point = 1.47 N

Example – 04:

A stone weighing 1 kg is whirled in a vertical circle at the end of a rope of length 1 m. Find the tension in the string and velocity of the stone at a) lowest position b) midway when the string is horizontal c) topmost position to just complete the circle.

Given: Radius of circle = r =1 m, mass of the body = m = 1 kg, g = 9.8 m/s²,

To find: Tension at lowest point = T_L = ?, Tension when string is horizontal = T_M = ?, Tension at topmost point = T_H = ?, velocity at lowest point = v_L = ?, velocity when string is horizontal = v_M = ?, velocity at topmost point = v_H = ?

Solution:

Ans: Velocity of stone at the lowermost point = 7 m/s, Velocity of stone when string is horizontal = 5.42 m/s, Velocity of stone at topmost point = 3.13 m/s, Tension at lowermost point = 58.8 N, Tension when string is horizontal = 0 N, Tension at topmost point = 29.4 N

Example – 05:

An object of mass 0.5 kg attached to a string of length 0.5 m is whirled in a vertical circle at constant angular speed if the maximum tension in the string is 5 kg wt. Calculate the speed of the object and maximum number of revolutions it can complete in one minute

Given: Mass of object = m = 0.5 kg, Radius of circle = r = 0.5 m, Tension in the string = T = 5 kg wt = 5 x 9.8 N.

To Find: Speed of the object = ?, the maximum number of revolutions per minute = N =?

Solution:

In vertical circle maximum tension is at the lowermost point

Ans: Speed of object = 6.64 m/s and maximum number of revolutions = 126.7 r.p.m.

Example – 06:

A pilot of mass 75 kg in a jet aircraft while executing a loop the loop with a constant speed of 360 km/h. If the radius of a circle is 200, compute the force exerted by seat on the pilot a) at the top of loop b) at the bottom loop.

Given: mass of piolot = m = 75 kg, radius of circle = r = 200 m, velocity of plane = v =360 km/h = 360 x 5/18 = 100 m/s  ,

To find: force at the top of loop = F_T =? Force at bottom of loop = F_B = ?,.

Solution:

At the topmost point, the centrifugal force acts vertically upward and the weight of the body acts vertically downward. Thus the net force on the pilot by the seat is given by

At the bottom-most point, both the centrifugal force and the weight of the body act vertically downward. Thus the net force on the pilot by the seat is given by

Ans: The force exerted by the seat on the pilot at the topmost point is 3015 N, The force exerted by the seat on the pilot at the bottom-most point is 4485 N.

Example – 07:

A pilot of mass 50 kg in a jet aircraft while executing a loop the loop with a constant speed of 250 m/s. If the radius of circle is 5 km, compute the force exerted by sent on the pilot a) at the top of loop b) at the bottom loop.

Given: mass of piolot = m = 50kg, radius of circle = r = 5 km = 5000 m, velocity of plane = v = 250 m/s,

To find: force at the top of loop = F_T =?, Force at bottom of loop = F_B = ?,.

Solution:

At the topmost point, the centrifugal force acts vertically upward and the weight of the body acts vertically downward. Thus the net force on the pilot by the seat is given by

At the bottom-most point, both the centrifugal force and the weight of the body act vertically downward. Thus the net force on the pilot by the seat is given by

Ans: The force exerted by the seat on the pilot at the topmost point is 135 N, The force exerted by the seat on the pilot at the bottom-most point is 1115 N.

Example – 08:

A ball is released from a height h along the slope and at the end of a slope moves along a circular track of radius R without falling vertically downwards. Determine the height h in terms of R.

Solution:

As the ball is released from a height along the slope and moves along a circular track thus it is looping a loop or it has sufficient velocity at the lowest point to loop a loop.

At lowest point, v = √5gr

By the law of conservation of energy

Potential energy at P = Kinetic energy at Q

Example – 09:

• A block of mass 1 kg is released from point P on a frictionless track which ends in a quarter-circular track of radius 2m at the bottom. What is the magnitude of radial acceleration and total acceleration of the block when it arrives at Q?

• Given: Height of point P above datum = 6 m, Radius of circular track = 2 m
• To find: the magnitude of radial acceleration = a_R = ? and magnitude of total acceleration = a =?
• Solution:

By the principle of conservation of energy

Total Energy at P = Total energy at Q

The magnitude of the radial acceleration is given by

At point Q the tangential acceleration is the acceleration due to gravity

Ans: Magnitude of radial acceleration = 39.2 m/s² and the magnitude of total acceleration = 40.4 m/s².

Example – 10:

A 3 kg ball is swung in a vertical circle at the end of an inextensible string 3 m long. What is the maximum and minimum tension in the string if the ball moves 90/π revolutions per minute.

Given: Mass of body = m = 3 kg, radius of circle = r = 3 m, rpm = N = 90/π r.p.m.  ,

To find: Maximum tension = T_max =? minimum tension = T_min = ?,

Solution:

At the bottom-most point, the centrifugal force acts vertically downward and the weight of the body acts vertically downward. Thus the tension in the string is maximum.

T_max = mrω² + mg = 3 x 3 x (3)² + 3 x 9.8 = 110.4 N

At the topmost point, the centrifugal force acts vertically upward and the weight of the body acts vertically downward. Thus the tension in the string is minimum.

T_min = mrω² – mg = 3 x 3 x (3)² – 3 x 9.8 = 51.6 N

Ans: Maximum tension at the bottom-most point is 110.4 N, Minimum tension at the topmost point is 51.6 N.

Example – 11:

A 2 kg ball is swung in a vertical circle at the end of an inextensible string 2 m long. What are the speed and angular speed of the ball if the string can sustain maximum tension of 119.6 N.

Given: Mass of body = m = 2 kg, radius of circle = r = 2 m, Maximum tension = T = 119.6 N,

To find: Linear speed = v =? angular speed = ω = ?

Solution:

At the bottom-most point, the centrifugal force acts vertically downward and the weight of the body acts vertically downward. Thus the tension in the string is maximum.

Ans: Maximum linear speed = 10 m/s, Maximum angular speed = 5 rad/s.

Previous Topic: The Concept of Conical Pendulum

For More Topics in Physics Click Here

Science > Physics > Circular Motion > Motion in Vertical Circle