Science > Physics > Introduction to Measurements > Measurement and its Need
Physics is a science of measurement. In this article, we shall study the meaning of the term ‘measurement’ and its importance in the field of science and engineering.
“When you can measure what you are speaking about and express it in numbers, you know something about it; but when you cannot express it in numbers, your knowledge is meagre and of an unsatisfactory kind.” – Lord Kelvin
LIST OF SUB-TOPICS:
- 1.2.1.1.1 ntroduction
- 1.2.1.1.2 Need for Measurement
- 1.2.1.1.3 Types of Measurement
- 1.2.1.1.4 Units of Measurement
- 1.2.1.1.5 Criteria for a Selection of Unit
- 1.2.1.1.6 Requirements of Standard
- 1.2.1.1.7 Old Methods of Measurements
- 1.2.1.1.8 Some Ancient Systems of Measurements
- 1.2.1.1.9 Need for Standard System of Units
- 1.2.1.1.10 Types of Physical Quantities
1.2.1.1.1 Measurements:
A measurement is a quantitative description of one or more fundamental properties compared to a standard. The measurement of a quantity is mentioned in two parts, the first part gives how many times the standard unit and the second part gives the name of the unit e.g. 5 m.
The numerical value of a physical quantity is inversely proportional to its unit. For example: centimetre (cm) is a smaller unit compared to metre (m) and 5 m = 500 cm. We can see that the larger number is associated with the smaller unit and the smaller number is associated with the larger unit. If n1 and n2 are the numerical values of a physical quantity in two different units say u1 and u2 respectively. The measure of a physical quantity depends on the system of units used. Then
n1 (u1) = n2 (u2)
1.2.1.1.2 Need for Measurement:
Measurement is crucial in various aspects of human life and across different fields. Here are some key reasons why measurement is essential:
- Quantification and Precision: Measurement allows us to quantify and express the attributes or characteristics of objects, events, or phenomena in a precise and standardized manner. It provides a common language for communication, ensuring that everyone understands and interprets values consistently.
- Scientific Research: In scientific research, accurate measurements are essential for conducting experiments, collecting data, and drawing meaningful conclusions. Precise measurements contribute to the reliability and reproducibility of scientific studies.
- Engineering and Technology: In engineering and technology, measurements are fundamental for designing, building, and testing various products and systems. Engineers rely on measurements to ensure the functionality, safety, and quality of their creations.
- Commerce and Trade: Measurement is crucial in commerce for standardizing transactions and trade. Standard units of measurement facilitate fair and transparent exchange of goods and services. Accurate measurements prevent misunderstandings and disputes in business transactions.
- Healthcare: In healthcare, measurements are used for diagnosing conditions, monitoring patient health, and administering treatments. Vital signs, laboratory results, and other medical measurements help healthcare professionals make informed decisions.
- Education: Measurement is a fundamental concept in education, providing a basis for assessing and evaluating students’ progress and achievements. Grading systems, standardized tests, and educational assessments rely on measurements.
- Quality Control: In manufacturing and production, measurements are crucial for quality control. They ensure that products meet specified standards and comply with regulations. Precise measurements help identify defects and improve the overall quality of products.
- Navigation: Measurements, such as distance and direction, are essential for navigation. They are used in various fields, including aviation, maritime, and land-based transportation.
- Environmental Monitoring: Measurement is vital for monitoring environmental factors, such as air and water quality, climate change, and biodiversity. Accurate measurements help in understanding and addressing environmental issues.
- Personal and Everyday Life: In our daily lives, we use measurements for cooking, construction, home improvement, and various other activities. Measurements provide a basis for making informed decisions, whether it’s choosing the right size clothing or determining the right amount of ingredients for a recipe.
Thus, measurement is a fundamental aspect of human endeavors, enabling us to understand, quantify, and interact with the world around us in a meaningful and standardized way.
1.2.1.1.3 Types of Measurements:
Depending on the method, measurements are classified into two types: a) Direct measurement and b) Indirect measurement
Direct Measurement:
When measurements are taken directly using tools, instruments, or other calibrated measuring devices, they are called direct measurements.
Examples of Direct Measurements:
- Length Measurement with a Ruler
- Temperature Measurement with a Thermometer
- Mass Measurement with a Balance
- Time Measurement with a Clock
- Voltage Measurement with a Voltmeter
- Volume Measurement with a Graduated Cylinder
- Pressure Measurement with a Pressure Gauge
- Speed Measurement with a Speedometer
- Force Measurement with a Spring Scale
- Concentration Measurement with a Spectrophotometer
- Sound Level Measurement with a Decibel Meter
- Electrical Current Measurement with an Ammeter:
These examples illustrate how direct measurements involve the use of specialized instruments or devices to obtain precise numerical values of various physical quantities. Direct measurements are essential for accurate and reliable data in scientific and everyday contexts
Indirect Measurement:
When the measurement must be done through a formula or other calculations, the measurement is called indirect measurement e.g. Measurement of the radius of the Earth.
Examples of Indirect Measurements:
- Distance Measurement using Trigonometry
- Determination of Acceleration Due to Gravity
- Estimating the Earth’s Circumference
- Calculating Density
- Determining the Speed of Sound
- Indirect Measurement of Magnetic Field Strength
- Estimating the Size of Atoms
- Determining the Mass of Celestial Bodies
- Indirect Measurement of Voltage in a Circuit
- Indirect Measurement of Blood Flow
- Determining the Height of a Building:
These examples demonstrate how indirect measurements are often employed when direct measurements are impractical or impossible. They rely on established principles, mathematical relationships, or models to infer the desired quantity indirectly.
1.2.1.1.4 Units of Measurements:
For any measurement, a number and unit are required. When we say that the time is 5 seconds, then we mean that the said time is 5 times a certain standard time called 1 second.
A unit is a selected magnitude of a physical variable in terms of which other magnitudes of the same variable can be expressed. Measurement without unit has no meaning.
1.2.1.1.5 Criteria for a Selection of Unit:
The selection of units in physics is crucial for clear communication, consistency, and ease of understanding. Scientists and engineers adhere to certain criteria when choosing units for various physical quantities. Here are some key criteria for selecting units in physics:
- Relevance to the Quantity Being Measured: The unit should be relevant and appropriate to the physical quantity being measured. For example, measuring length in meters, mass in kilograms, and time in seconds are common and logical choices.
- Magnitude of Quantity: The selection of a unit depends on the magnitude of a quantity under consideration. For e.g. when we are measuring the diameter of a rod we should use millimetre as a unit. When we are measuring the height of a tower we should use the metre as a unit. When we are measuring the distance between the two cities we should use kilometre as a unit. When we are measuring the distance between the two stars we should use light-years as a unit. This clearly indicates that when the magnitude of the measurement increases, then the unit used for the measurement should be larger. The unit should be neither too small nor too big in comparison with the physical quantity to be measured.
- Degree of Accuracy: The accuracy of measurement also influences the selection of the unit. In the case of construction of a room where accuracy is not a major criteria metre or foot are used as units. But when constructing a rocket, accuracy is important hence millimetre or micrometre may be the unit. Thus when the accuracy is important then the unit used for the measurement should be smaller.
- Consistency within the System: Units within a system should be consistent with each other. In the International System of Units (SI), there is a standardized set of units and prefixes that ensures consistency across different physical quantities.
- Ease of Measurement: Units should be convenient and practical for measurement. For instance, using the meter for measuring length instead of a smaller or larger unit makes measurements more manageable.
- Avoidance of Ambiguity: Units should be unambiguous and easily understood. Using well-defined units helps prevent confusion and misinterpretation of measurements.
- Avoidance of Redundancy: Redundant or unnecessary units should be avoided. For example, using both kilometers and meters to express length in the same context may lead to confusion.
- Interchangeability and Coherence: Units should be interchangeable and coherent. Coherence ensures that equations are mathematically consistent, and units can be manipulated algebraically.
- Alignment with Standards: Units should align with international standards. The International System of Units (SI) is a globally accepted system that provides a standardized set of units for various physical quantities.
- Avoidance of Arbitrary Factors: Units should not involve arbitrary factors. Using natural constants or standard physical properties (like the speed of light) in defining units adds reliability and universality.
- Historical and Cultural Considerations: In some cases, historical or cultural factors may influence the choice of units. However, contemporary science and engineering typically favor standardized units for consistency and global collaboration.
- Adaptability to Technology: Units should be adaptable to advancements in technology. As technology evolves, units may need to be updated or revised to accommodate new measurement capabilities.
- Ease of Calculations: Units that simplify calculations and reduce the need for conversion factors are preferred. This makes mathematical operations more straightforward.
- Global Acceptance: Units that are widely accepted on a global scale facilitate communication and collaboration among scientists, engineers, and researchers worldwide.
The adherence to these criteria ensures that units used in physics are standardized, consistent, and well-suited for expressing and comparing physical quantities accurately. The adoption of the SI system reflects the commitment to these criteria in the field of physics and related disciplines.
1.2.1.1.6 Requirements of Standard:
The establishment of standards of measurement is essential for ensuring consistency, accuracy, and uniformity in various fields of science, engineering, commerce, and everyday life. The requirements for a standard of measurement include:
- Accuracy: A standard of measurement must provide accurate and reliable results. It should be based on precise and well-defined criteria to minimize errors in measurements.
- Consistency: A standard should not change with the place. This concept is known as uniformity or consistency and is crucial for ensuring that measurements are reliable, comparable, and consistent regardless of the location where they are taken.
- Non-Destructibility: The requirement that a standard should be non-destructible is important for the sustainability and longevity of measurement standards. Efforts are made in the development of standards to choose materials and designs that minimize degradation over time. However, the goal of achieving a truly non-destructible standard may be challenging due to factors like wear, aging, and environmental influences.
- Stability: The standard should remain stable over time and not undergo significant changes. Stability is crucial for ensuring the long-term reliability and consistency of measurements.
- Reproducibility: The standard must be reproducible, meaning that the same measurement can be obtained by different observers using the same standard and measurement procedures. This ensures consistency across different laboratories and locations.
- Invariability: A standard should be invariant under specified conditions. This means that its properties do not change with variations in environmental factors like temperature, pressure, or humidity.
- Accessibility: The standard should be easily accessible to the scientific and industrial communities. This often involves the widespread distribution of measurement standards or the establishment of international organizations responsible for maintaining and disseminating standards.
- Universality: Ideally, a standard should be universally accepted and recognized. This promotes consistency and facilitates international collaboration in scientific research, trade, and various other fields.
- Definability: The standard should have a clear and unambiguous definition, often expressed in terms of fundamental constants or physical properties that can be precisely measured.
- Traceability: Traceability ensures that measurements can be linked back to a known reference, providing a transparent and auditable chain of measurements. This is particularly important for maintaining the integrity and reliability of measurements.
- Practicality: Standards should be practical to use in real-world applications. This involves considerations such as ease of implementation, cost-effectiveness, and compatibility with existing technologies and practices.
- Comprehensiveness: Standards should cover a broad range of physical quantities and be adaptable to different measurement needs. Comprehensive standards support a wide variety of scientific, industrial, and commercial activities.
- International Acceptance: Global standards are essential for international cooperation and trade. Standards that are widely accepted and adopted by different countries help ensure consistency in measurements on a global scale.
- Review and Update: Standards need periodic review and, if necessary, updating to incorporate new knowledge, advancements in technology, and changes in measurement practices.
- Legal Recognition: Many standards are legally recognized to ensure their enforceability and to provide a basis for regulatory compliance. Legal recognition helps maintain consistency and fairness in various industries and applications.
- Educational Support: Standards should be supported by educational programs and training to ensure that individuals involved in measurements understand and adhere to established practices.
By meeting these requirements, standards of measurement contribute to the reliability, comparability, and integrity of measurements across diverse applications and disciplines.
Characteristics of Standard Unit:
- It should be well defined without any doubt or ambiguity.
- It should be of suitable size. i.e. neither too long nor too small in comparison with quantity to be measured.
- It should be easily available.
- It should be non-destructible.
- It should not change with time.
- It should not change with the place.
- It should be easily reproducible.
1.2.1.1.7 Old Methods of Measurements:
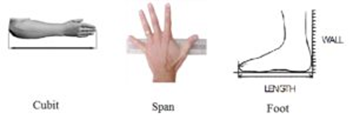
To measure
lengths units used were a finger, palm, span, cubit, foot, yard, fathom,
furlong etc.
1 finger = 1 digit, 4 digits = 1 palm, 2 palms = 1 span, 2 spans = 1 cubit.
- 1 furlong: It was a length of a furrow an ox (Bullock) could plough without rest.
- 1 furlong = 220 yards
- 1 furlong = 0.201168 km
- 1 acre: It is an area an ox can plough in a day.
- 1 acre = 4840 sq. yards
- 1 acre = 40000 sq. feet

We can see that, these standards may vary from person to person and animal to animal. Hence these units and standards were non-reliable. In 1799 after the revolution the new republic of France accepted a metric system based on centimetre, gram and second (c.g.s. system). Britain accepted this system in 1852 for scientific purposes only. A committee consisting of chemist Antoine Laurent de Lavoisier and mathematician Joseph Louis Lagrange suggested the decimal system for measurement.
In 1901 Italian engineer Giovanni Giorgi suggested a metric system based on the metre, kilogram and second (M.K.S. system). It was upgraded to the S.I. system by adding some more fundamental units in 1960.
1.2.1.1.8 Some Ancient Systems of Measurements:
Ancient civilizations developed their own systems of measurement based on the practical needs of their societies. These systems varied widely across different cultures and regions. Here are some examples of ancient systems of measurement:
- Egyptian System: The ancient Egyptians used a system of measurements based on body parts and natural objects. The cubit, defined as the length from the elbow to the tip of the middle finger, was a fundamental unit. Other units included the digit (finger width) and the palm (width of the hand).
- Mesopotamian System: Mesopotamian civilizations, such as the Sumerians and Babylonians, used a sexagesimal (base-60) system for counting and measuring. The Babylonian system included units like the digit, finger, hand, foot, and cubit.
- Roman System: The ancient Romans had a system of measurements that included units such as the digit (1/16 of a foot), palm (4 digits), foot (pes), cubit (cubitum), and pace (double step). The Roman foot, roughly equivalent to 29.6 cm, was commonly used.
- Greek System: Ancient Greeks had various units for measuring length, including the foot (pous), cubit (pechys), and stadium (stade). The Greeks also developed geometric methods to measure distances indirectly.
- Chinese System: Traditional Chinese units of measurement varied across different regions and dynasties. Units included the chi (foot), zhang (pace), and li (mile). The standardization of Chinese measurements occurred at various times in history.
- Indus Valley System: The ancient Indus Valley Civilization had its own system of measurements, as evidenced by artifacts found at archaeological sites. The unit known as the “Indus inch” has been identified.
- Mayan System: The ancient Mayans used a vigesimal (base-20) counting system. Their system of measurement included units for length and time, with the “pop” representing 20 and the “bak’tun” representing 400.
- Hebrew System: The ancient Hebrews had a system of measurements described in the Hebrew Bible. Units included the cubit, handbreadth, span, and shekel.
- Persian System: The ancient Persian system of measurements included units such as the hasta (cubit), dana (weight), and drahma (volume). The Persian system influenced neighboring cultures.
- Aztec System: The Aztecs, in Mesoamerica, had their own system of measurement. Units included the tlalquahuitl (rod) and the calli (house) as a measure of area.
It’s important to note that the precision and standardization of these ancient systems were often limited compared to modern standards. Additionally, different regions and time periods within these civilizations may have used slightly different variations of these systems. The move towards more standardized and globally accepted systems of measurement, such as the International System of Units (SI), has been a more recent development in human history.
1.2.1.1.9 Need for Standard System of Units:
When humans became civilised, started cultivating and living in communities they realised that one cannot do everything and they need to be interdependent. This paved the way for trade and then probably a need for a measure was felt. The recorded history shows ample evidence that the different parts of the human body were used as a point of reference while making measurements. The units based on parts of the human body are arbitrary and inaccurate. The results of the measurements vary from person to person because the size of the unit is different for a different person. This created problems in trade between different countries and also in the day to day transactions.
The need for a standard system of units is critical for several reasons, spanning scientific, technological, industrial, commercial, and everyday applications. The adoption of a standard system of units provides a universal and consistent framework for measurement, offering the following benefits:
- Consistency and Uniformity: A standard system of units ensures consistency and uniformity in measurements across different disciplines, industries, and geographical regions. This consistency is essential for accurate communication and understanding.
- Global Collaboration: Standard units facilitate global collaboration in scientific research, engineering, and trade. Researchers and professionals from different countries can easily share and compare data, contributing to international progress.
- Facilitates Communication: Standard units provide a common language for expressing measurements. This facilitates effective communication among scientists, engineers, manufacturers, and other stakeholders, reducing the risk of misinterpretation.
- Trade and Commerce: In commerce, having a standard system of units is crucial for fair and transparent transactions. Standardized measurements contribute to trust and prevent misunderstandings in trade and commercial exchanges.
- Ease of Conversion: A standard system simplifies the conversion of units. Conversions between different units within the same system are straightforward, promoting efficiency in various applications.
- Interdisciplinary Integration: Different scientific and engineering disciplines often work together on complex projects. A standard system of units facilitates interdisciplinary integration, allowing professionals from various fields to collaborate seamlessly.
- Education and Training: Standard units are fundamental to education and training in science and engineering. They provide a consistent framework for teaching and learning, ensuring that students develop a universal understanding of measurements.
- Quality Control and Assurance: Standard units are essential for quality control and assurance in manufacturing and industry. They ensure that products meet specified standards and adhere to regulatory requirements.
- Safety and Regulation: Many safety regulations and standards rely on standardized measurements. This is particularly important in industries where precision and accuracy are critical to ensuring the safety of products and processes.
- Scientific Reproducibility: Standard units are crucial for the reproducibility of scientific experiments. Researchers need a common basis for reporting results, allowing others to replicate experiments and validate findings.
- Technological Innovation: Technological advancements often rely on standardized measurements. A consistent system of units supports innovation by providing a reliable framework for designing, testing, and implementing new technologies.
- Public Understanding: A standard system of units helps the general public understand measurements in everyday contexts. It simplifies communication of quantities such as length, weight, and volume, making information more accessible.
- International Trade Agreements: Many international trade agreements and standards organizations require the use of standardized measurements to facilitate cross-border trade and ensure fairness.
To overcome the limitations of body parts as units, and to bring about uniformity in the measurement system, the need for exact measurement was felt. For this, a standard of measurement had to be developed that is acceptable to everybody and to make our judgment more reliable and accurate. Thus there should be uniformity in measurement. For the sake of uniformity, we need a common set of units of measurement, which are called standard units. The International System of Units (SI) is the most widely adopted standard system of units globally. It provides a comprehensive and coherent set of units for measuring physical quantities, and its adoption has significantly contributed to the advancement of science, technology, and global collaboration.
1.2.1.1.10 Types of Physical Quantities:
Physical quantities are those quantities that are measurable. The Physical quantities are classified as a) Fundamental quantities and b) Derived quantities
Fundamental Quantities:
Fundamental quantities are those quantities which do not depend on other quantities for their measurements. The units of fundamental quantities are called fundamental units. For Example mass, length, time etc. are fundamental quantities, while, their units metre, kilogram, second etc. are fundamental units.
Fundamental units can neither be derived from one another nor can they be further resolved into other simpler units.
Derived Quantities:
Derived quantities are those quantities that depend on two or more other quantities for their measurements. The units of derived quantities are called derived units. For example, density, acceleration, velocity, force, momentum, pressure, etc. are derived quantities, while, their units kg m-3, m s-2, m s-1, newton, kg-m s-1, pascal, etc. are derived units.
Conclusion:
Measurement is the process of assigning a numerical value to a physical quantity. It involves comparing an unknown quantity to a standard unit of measurement, resulting in a numerical representation of the quantity’s magnitude. Measurements are fundamental in various scientific, industrial, and everyday contexts, providing a basis for understanding, quantifying, and communicating physical phenomena. Measurement serves as a foundational tool for understanding the physical world, making informed decisions, and driving advancements in science, technology, industry, and daily life.
Related Topics:
- 1.2.1 Introduction to Measurements
- 1.2.2 Meassurement of Length, Area and Volume
- 1.2.3 Measurement of Mass, Weight, and Density
- 1.2.4 Measurement of Time
- 1.2.5 Dimensional Analysis
- 1.2.6 Error Analysis
One reply on “1.2.1.1 Measurement and its Need”
Nice and educative