Science > Physics > Elasticity > Numerical Problems on Poisson’s Ratio
In this article, we shall study the concept of poisson’s ratio and numerical problems on it. The concept of this constant (Poisson,s ratio) was introduced by physicist Simeon Poisson. When a rod or wire is subjected to tensile stress, its length increases in the direction of stress, but its transverse (lateral) dimensions decrease and vice-versa. i.e. when the length increase, the thickness decreases and vice-versa. In other words, we can say that the longitudinal strain is always accompanied by a transverse (lateral) strain.
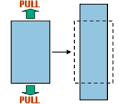
The ratio of transverse strain to the corresponding longitudinal strain is called Poisson’s ratio. It is denoted by letter ‘m’. It has no unit. It is a dimensionless quantity.
Poisson’s Ratio = Lateral strain / Longitudinal strain
For homogeneous isotropic medium -1 ≤ m ≤ 0.5. In actual practice, Poisson’s ratio is always positive. There are some materials with a negative Poisson’s ratio. Poisson’s ratio of cork is zero, that of metal is 0.3 and that of rubber is 0.5.
Materials with a negative value of Poisson’s ratio are said to be auxetic. They grow larger in the transverse direction when stretched and smaller when compressed. Most auxetic materials are polymers with a crumpled, foamy structure. Pulling the foam causes the crumples to unfold and the whole network expands in the transverse direction.
Numerical Problems:
Example – 1:
When a brass rod of diameter 6 mm is subjected to a tension of 5 × 103 N, the diameter changes by 3.6 × 10-4 cm. Calculate the longitudinal strain and Poisson’s ratio for brass given that Y for the brass is 9 × 1010 N/m².
Given: Diameter of rod = D = 6 mm, Radius of wire = 6/2 = 3 mm = 3 × 10-3 m, Load F = 5 × 103 N, Change in diameter = d = 3.6 × 10-4 cm = 3.6 × 10-6 m, Y for the brass is 9 × 1010 N/m².
To Find: Longitudinal strain =? Poisson’s ratio = ?,
Solution:
Y = Longitudinal Stress /Longitudinal Strain
∴ Y = F / (A × Longitudinal Strain)
∴ Longitudinal Strain = F / (A × Y)
∴ Longitudinal Strain = F / (π r² × Y)
∴ Longitudinal Strain = 5 × 103 / (3.142 × (3 × 10-3)² × 9 × 1010)
∴ Longitudinal Strain = 5 × 103 / (3.142 × 9 × 10-6 × 9 × 1010)
∴ Longitudinal Strain = 1.96 × 10-3
Now, Lateral strain = d /D = (3.6 × 10-6)/ (6 × 10-3) = 6 × 10-4
Poisson’s ratio = Lateral strain / Longitudinal strain
∴ Poisson’s ratio = (6 × 10-4) / (1.96 × 10-3) = 0.31
Ans: Longitudinal strain is 1.96 × 10-3 and Poisson’s ratio is 0.31.
Example – 2:
A metal wire of length 1.5 m is loaded and an elongation of 2 mm is produced. If the diameter of the wire is 1 mm, find the change in the diameter of the wire when elongated. σ = 0.24.
Given: Original length of wire = L = 1.5 m, Elongation in wire = 2 mm = 2 × 10-3 m, Diameter of wire = D = 1 mm, Poisson’s ratio = σ = 0.24.
To Find: Change in diameter = d =?
Solution:
Longitudinal strain = l/L = (2 × 10-3)/1.5 = 1.33 × 10-3
Poisson’s ratio = Lateral strain / Longitudinal strain
∴ Lateral strain =Poisson’s ratio × Longitudinal strain
∴ Lateral strain = 0.24 × 1.33 × 10-3 = 3.2 × 10-4
Lateral strain = d / D
∴ d = Lateral strain × D = 3.2 × 10-4 × 1 × 10-3 = 3.2 × 10-7 m
Ans: The change in diameter is 3.2 × 10-7 m
Example – 3:
A metallic wire (Y = 20 × 1010 N/m². and σ = 0.26) of length 3 m and diameter 0.1 cm is stretched by a load of 10 kg. Calculate the decrease in diameter of the wire.
Given: Original length of wire = L = 3 m, Diameter of wire = D = 0.1 cm = 0.1 × 10-2 m = 1 × 10-3 m, Radius of wire = r = 0.1/2 = 0.05 cm = 0.05 × 10-2 m = 5 × 10-4 m,, Stretching load = 10 kg = 10 x 9.8 N, Young’s modulus of elasticity = Y = 20 × 1010 N/m², and Poisson’s ratio = σ = 0.26
To Find: Decrease in diameter = d =?
Solution:
Y = Longitudinal Stress /Longitudinal Strain
∴ Y = F / (A × Longitudinal Strain)
∴ Longitudinal Strain = F / (A × Y)
∴ Longitudinal Strain = F / (π r² × Y)
∴ Longitudinal Strain = (10 x 9.8) / (3.142 × (5 × 10-4)² × 20 × 1010)
∴ Longitudinal Strain = (10 x 9.8) / (3.142 × 25 × 10-8 × 20 × 1010)
∴ Longitudinal Strain = 6.24 × 10-4
Poisson’s ratio = Lateral strain / Longitudinal strain
∴ Lateral strain =Poisson’s ratio × Longitudinal strain
∴ Lateral strain = 0.26 × 6.24 × 10-4 = 1.62 × 10-4
Lateral strain = d / D
∴ d = Lateral strain × D = 1.62 × 10-4 ×1 × 10-3 = 1.62 × 10-7 m
Ans: The decrease in diameter is 1.62 × 10-7 m
Example – 4:
A copper wire 3m long and 1 mm² in cross-section is fixed at one end and a weight of 10 kg is attached at the free end. If Y for copper is 12.5 × 1010 N/m² and σ = 0.25 find the extension, lateral strain and the lateral compression produced in the wire.
Given: Original length of wire = L = 3 m, Area of cross-section of wire = A = 1 mm² = 1 × 10-6 m², Stretching load = 10 kg = 10 × 9.8 N, Young’s modulus of elasticity = Y = 12.5 × 1010 N/m², and Poisson’s ratio = σ = 0.25
To Find: Extension = l =? Lateral strain = ?, Lateral compression = ?
Solution:
Y = Longitudinal Stress /Longitudinal Strain
∴ Y = F / (A × Longitudinal Strain)
∴ Longitudinal Strain = F / (A × Y)
∴ Longitudinal Strain = 10 × 9.8 / (1 × 10-6 × 12.5 × 1010)
∴ Longitudinal Strain = 10 × 9.8 / (1 × 10-6 × 12.5 × 1010)
∴ Longitudinal Strain = 7.84 × 10-4
Now, Longitudinal Strain = l/L
∴ l = Longitudinal strain × L
∴ l = 7.84 × 10-4 × 3 =2.352 × 10-3 m = 2.352 mm
Poisson’s ratio = Lateral strain / Longitudinal strain
∴ Lateral strain =Poisson’s ratio × Longitudinal strain
∴ Lateral strain = 0.25 × 7.84 × 10-4 = 1.96 × 10-4
Area of cross-section = A = 1 × 10-6 m²
∴ π r² = 1 × 10-6
∴ r² = 1 × 10-6/ π = = 1 × 10-6/ 3.142
∴ r² = 0.3183 × 10-6
∴ r = 5.64 × 10-4 m
Diameter = D = 2r = 2 × 5.64 × 10-4 m = 11.28 × 10-4 m
Now, Lateral strain = d / D
∴ d = Lateral strain × D = 1.96 × 10-4 × 11.28 × 10-4 = 2.21 × 10-7 m
Ans: Elongation = 2.352 mm, Lateral strain = 1.96 × 10-4, Lateral compression = 2.21 × 10-7 m.
Example – 5:
A wire of diameter 2 mm and length 5 m is stretched by a load of 10 kg. Find the extension produced in the wire if Y = 12 × 1010 N/m². If σ = 0.35 for the material of the wire, find the lateral contraction.
Given: Original length of wire = L = 5 m, Diameter of wire = D = 2 mm = 2 × 10-3 m , Radius of wire = 2/2 = 1mm = 1 × 10-3 m, Stretching load = 10 kg = 10 × 9.8 N, Young’s modulus of elasticity = Y = 12 × 1010 N/m², and Poisson’s ratio = σ = 0.35
To Find: Lateral contraction =?
Solution:
Y = Longitudinal Stress /Longitudinal Strain
∴ Y = F / (A × Longitudinal Strain)
∴ Longitudinal Strain = F / (A × Y)
∴ Longitudinal Strain = F / (π r² × Y)
∴ Longitudinal Strain = (10 x 9.8) / (3.142 × (1 × 10-3)² × 12 × 1010)
∴ Longitudinal Strain = (10 x 9.8) / (3.142 × 1 × 10-6 × 12 × 1010)
∴ Longitudinal Strain = 2.6 × 10-4
Now, Longitudinal Strain = l/L
∴ l = Longitudinal strain × L
∴ l = 2.6 × 10-4 × 5 = 1.3 × 10-3 m = 1.3 mm
Poisson’s ratio = Lateral strain / Longitudinal strain
∴ Lateral strain =Poisson’s ratio × Longitudinal strain
∴ Lateral strain = 0.35 ×2.6 × 10-4 = 9.1 × 10-5
Now, Lateral strain = d / D
∴ d = Lateral strain × D = 9.1 × 10-5 × 2 × 10-3 = 1.82 × 10-7 m
Ans: Elongation = 1.3 mm, Lateral contraction = 1.82 × 10-7 m
Example – 6:
Find the longitudinal stress to be studied to a wire to decrease its diameter uniformly by 1%. Poisson’s ratio = 0.25, Young’s modulus = 2 × 1011N/m².
Given: Lateral strain = 1 % = 1 × 10-2, Young’s modulus of elasticity = Y = 2 × 1011 N/m² . and Poisson’s ratio = σ = 0.25
To Find: Longitudinal stress =?
Solution:
Poisson’s ratio = Lateral strain / Longitudinal strain
∴ Longitudinal strain =Lateral strain / Poisson’s ratio
∴ Longitudinal strain = 1 × 10-2 / 0.25 = 4 × 10-2
Y = Longitudinal Stress /Longitudinal Strain
∴ Longitudinal Stress = Longitudinal Strain × Y
∴ Longitudinal Stress = 4 × 10-2 × 2 × 1011 = 8 × 109 N/m² .
Ans: Longitudinal stress = 8 × 109 N/m²
Example – 7:
A copper wire 3 m long is stretched to increase its length by 0.3 cm. Find the lateral strain produced in the wire. If Poisson’s ratio for copper is 0.26.
Solution:
Given: Length of wire = L = 3m, Increase in length = l = 0.3 cm = 0.3 × 10-2 m = 3 × 10-3 m, Poisson’s ratio = σ = 0.26
To Find: Lateral strain =?
Longitudinal strain = l/L = (3 × 10-3)/ 3 = 10-3
Poisson’s ratio = Lateral strain / Longitudinal strain
∴ Lateral strain =Poisson’s ratio × Longitudinal strain
∴ Lateral strain = 0.36 × 10-3 = 3.6 × 10-4
Ans: Lateral strain = 3.6 × 10-4
Example – 8:
A steel wire having cross-sectional area 1 mm² is stretched by 10 N. Find the lateral strain produced in the wire. Young’s modulus for steel is 2 × 1011 N/m² and Poisson’s ratio is 0.291.
Solution:
Given: Area of cross-section = 1 mm² = 1 × 10-6 m², Stretching Load = 10 N, Young’s modulus for steel= Y = 2 × 1011 N/m², Poisson’s ratio = σ = 0.291
To Find: Lateral strain =?
Y = Longitudinal Stress / Longitudinal Strain
∴ Y = F / (A × Longitudinal Strain)
∴ Longitudinal strain = F / (A × Y)
∴ Longitudinal strain = 10 / (1 × 10-6 × 2 × 1011) = 5 × 10-5
Poisson’s ratio = Lateral strain / Longitudinal strain
∴ Lateral strain =Poisson’s ratio × Longitudinal strain
∴ Lateral strain = 0.291 × 5 × 10-5 = 1.455 × 10-5
Ans: Lateral strain =1.455 × 10-5
Example – 9:
A load 1 kg produces a certain extension in the wire of length 3 m and radius 5 × 10-4 m. How much will be the lateral strain produced in the wire? Given Y = 7.48 × 1010 N/m², σ = 0.291.
Solution:
Given: Load attached = F = 1 kg = 1 × 9.8 N, Length of wire = L = 3 m, Radius of cross-section = r = 5 × 10-4 m cross-section = 1 mm² = 1 × 10-6 m², Stretching Load = 10 N, Young’s modulus = Y = 7.48 × 1010 N/m², Poisson’s ratio = σ = 0.291
To Find: Lateral strain =?
Y = Longitudinal Stress / Longitudinal Strain
∴ Y = F / (A × Longitudinal Strain)
∴ Y = F / (π r² × Longitudinal Strain)
∴ Longitudinal strain = (1 × 9.8) /(3.142 × (5 × 10-4)² × 7.48 × 1010)
∴ Longitudinal strain = (1 × 9.8) /(3.142 × 25 × 10-8 × 7.48 × 1010)
∴ Longitudinal strain = 1.67 × 10-4
Poisson’s ratio = Lateral strain / Longitudinal strain
∴ Lateral strain =Poisson’s ratio × Longitudinal strain
∴ Lateral strain = 0.291 × 1.67 × 10-4 = 4.86 × 10-5
Ans: Lateral strain = 4.86 × 10-5
Previous Topic: Numerical Problems on Stress, Strain, and Young’s Modulus
Next Topic: Numerical Problems on Stresses and Strains in Composite Wires
One reply on “Numerical Problems on Poisson’s Ratio”
I am happy now ,I can solve problems on poisson’s ratio .