Principles of Parallel and Perpendicular Axes

Science > Physics > Rotational Motion > Principles of Parallel and Perpendicular Axes

In this article, we shall study the principle of parallel axes and the principle of perpendicular axes and their applications.

Principle of Parallel Axes or Parallel Axes Theorem:

Statement :

The moment of inertia of a rigid body about any axis is equal to the sum of its moment of inertia about a parallel axis through its centre of mass and the product of the mass of the body and the square of the distance between the two axes.

Explanation :

Consider a rigid body of mass M rotating about an axis passing through point O and perpendicular to the plane of the paper. Let I_O be the moment of inertia of the body about the axis passing through O and perpendicular to the plane of the paper. Let IG be the moment of inertia of the body about the axis passing through the centre of mass of the body (G) and parallel to the given axis passing through O.

Let ‘h’ be the distance between the two axes i.e. (OG) = h. Then by the principle of parallel axes’

I_O = I_G +  Mh²

This is the mathematical statement of the principle of parallel axes.

Proof:                 

Consider the infinitesimal element of the body of mass   ‘dm’   at P, in the plane of the paper.  Join OP, OG, and GP.  Draw a perpendicular from P on extended line OG, such that PD ⊥ OG.

By definition of the moment of inertia

Applying Pythagoras theorem to Δ OPD

OP² =   OD² +  PD²

∴ OP²  =   (OG + GD)² + PD²

∴ OP² = OG²+2OG.GD + GD² + PD² …(3)

In DPGD, by Pythagoras theorem,

PG²  = GD² + PD²  ……..   (4)

From-equations (3) and (4)

OP² = OG² + 2 OG.GD + PG²

Multiplying both sides of the above equation by dm

dm.OP² = dm.OG² + 2 dm.OG.GD + dm.PG²

integrating both sides

I_O = I_G +  Mh² (Proved)

Principle of Perpendicular Axes or Theorem of Perpendicular axes:

Statement:

Moment of inertia of a rigid plane lamina about an axis perpendicular to its plane is equal to the sum of its moment of inertia about any two mutually perpendicular axes in its plane and meeting in the point where the perpendicular axis cuts the lamina.

Explanation:

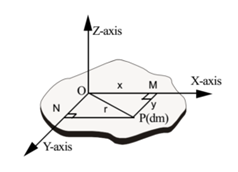
Consider a thin rigid plate or layer or lamina (in this case thickness of the body is less compared to its surface area). Let OX and OY be two mutually perpendicular axes in the plane of a rigid lamina, intersecting at O. Let OZ be, other axes which is passing through point O and is perpendicular to the plane of the lamina. Let l_x , l_y and I_z be the moments of Inertia of the lamina about OX, OY and OZ axes respectively.

Then by the principle of perpendicular axes,

l_z    =    l_x  +   l_y

This is the mathematical statement of the principle of perpendicular axes.

Proof:

Consider an infinitesimal element in the plane of lamina having mass dm situated at point P. Let the coordinates of point P be (x, y). Join OP and draw PM and PN perpendicular on OX and OY, respectively.

Then OM =  NP  =  x   and  MP = ON  =  y, Let OP  =  r

Moment of inertia of the lamina about Z-axis is given by

Similarly, M.I. of the lamina about X-axis is given by

Similarly Moment of Inertia of the lamina about Y-axis la given by

Applying Pythagoras theorem to triangle OPM

OP² =  OM² + PM²

∴ z² =  x² + y²

Multiplying both sides of the equation by dm and integrating

From equation (1), (2), (3) and (4)

l_z    =    l_x  +   l_y     (Proved)

Previous Topic: Kinetic Energy of Rotating Bofy

Next Topic: Derivation of Expressions for M.I.

Science > Physics > Rotational Motion > Principles of Parallel and Perpendicular Axes