Science > Physics > Rotational Motion > Numerical Problems on Moment of Inertia and Radius of Gyration
In this article, we shall study to solve problems of calculation of moment of inertia, the radius of gyration, and torque acting on a rotating body.
Example – 01:
A thin uniform rod of length 1 m and mass 1 kg is rotating about an axis passing through its centre and perpendicular to its length. Calculate the moment of inertia and radius of gyration of the rod about an axis passing through a point midway between the centre and its edge perpendicular to its length.
Given: Mass of rod = M = 1 kg, length of rod = l = 1m.
To Find: M.I. = I =? and radius of gyration = K =? at h = l/4
Solution:
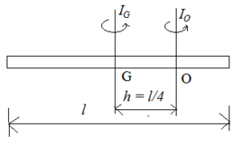
Moment of inertia of a thin uniform rod about a transverse axis passing through its centre is given by
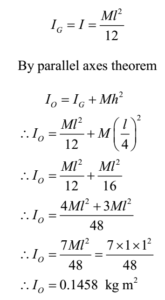
Now I = MK2
K2 = I/M = 0.1458/1 = 0.1458
K = 0.3818 m
Ans: M.I. about the required axis is 0.1458 kg m2, and radius of gyration is0.3818 m
Example – 02:
Calculate the M. I. of a thin uniform rod of mass 100g and length 60 cm about an axis perpendicular to its length and passing through (1) its centre and (2) one end.
Given: Mass of rod = M = 100 g = 0.1 kg, length of rod = l = 60 cm = 0.6 m.
Solution:
Moment of inertia of the thin uniform rod about a transverse axis passing through its centre is given by
I = Ml2/12 = 0.1 x (0.6)2/12 = 0.003 kg m2
Moment of inertia of the thin uniform rod about a transverse axis passing through its end is given by
I = Ml2/3 = 0.1 x (0.6)2/3 = 0.012 kg m2
Ans: Moment of inertia of the thin uniform rod about a transverse axis passing through its centre is 0.003 kg m2 and the moment of inertia of the thin uniform rod about a transverse axis passing through its end is 0.012 kg m2.
Example – 03:
Find the M. I. of a thin uniform rod 1 m long and weighing 0.024 kg about a transverse axis passing through (1) its centre (2) one end (3) a point 20 cm from one end.
Given: Mass of rod = M = 0.024 kg, length of rod = l = 1 m.
Solution:
Moment of inertia of the thin uniform rod about a transverse axis passing through its centre is given by
I = Ml2/12 = 0.024 x (1)2/12 = 0.002 kg m2
Moment of inertia of the thin uniform rod about a transverse axis passing through its end is given by
I = Ml2/3 = 0.024 x (1)2/3 = 0.008 kg m2
Moment of inertia of the thin uniform rod about a transverse axis passing through a point 20 cm from one end.
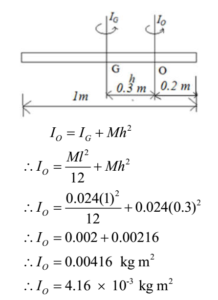
Ans: Moment of inertia of the thin uniform rod about a transverse axis passing through its centre is 0.002 kg m2, Moment of inertia of the thin uniform rod about a transverse axis passing through its end is 0.008 kg m2, Moment of inertia of the thin uniform rod about a transverse axis passing through a point 20 cm from one end is 4.16 x 10-3 kg m2
Example – 04:
A thin ring has mass 0.25 kg and radius 0.5 m. Calculate the moment of inertia about i) an axis passing through its centre and perpendicular to the plane and ii) an axis passing through a point on its circumference, perpendicular to its plane iii) diameter. iii) an axis tangent to ring and its plane
Given : Mass of Ring = M = 0.25 kg, Radius of ring = R = 0.5 m
Solution:
Moment of inertia about a transverse axis passing through its centre is given by
I = MR2 = 0.25 x (0.5)2 = 0.25 x 0.25 = 0.0625 kgm2
Moment of inertia about a transverse axis passing through its circumference is given by
I = 2MR2 = 2 x 0.25 x (0.5)2 = 2 x 0.25 x 0.25 = 0.125 kgm2
Moment of inertia about its diameter is given by
I = MR2/2 = 0.25 x (0.5)2/2 = 0.25 x 0.25/2 = 0.03125 kgm2
Moment of inertia about an axis tangent to the ring and its plane is given by
I = 3/2MR2 = 3/2 x (0.25 x (0.5)2) = 3/2 x (0.25 x 0.25) = 0.09375 kgm2
Ans: Moment of inertia about a transverse axis passing through its centre is 0.0625 kgm2. Moment of inertia about a transverse axis passing through its circumference is 0.125 kgm2. Moment of inertia about its diameter is 0.03125 kgm2. Moment of inertia about an axis tangent to the ring and its plane is 0.09375 kgm2
Example – 05:
Calculate the moment of inertia of a ring of mass 500 g and radius 0.5 m about an axis of rotation coinciding with its diameter and tangent perpendicular to its plane.
Given: Mass of Ring = M = 500 g = 0.5 kg, Radius of ring = R = 0.5 m
Solution:
Moment of inertia about its diameter is given by
I = MR2/2 = 0.5 x (0.5)2/2 = 0.5 x 0.25/2 = 0.0625 kgm2
Moment of inertia about an axis tangent to ring and perpendicular to its plane is given by
I = 2MR2 = 2 x 0.5 x (0.5)2 = 0.25 kgm2
Ans: Moment of inertia about its diameter is 0.0625 kgm2. Moment of inertia about an axis tangent to ring and perpendicular to its plane is 0.0625 kgm2
Example – 06:
Calculate the M.I. of a disc of mass 0.5 kg and radius 10 cm about an axis passing through its centre and at right angles to its plane. What would be the M. I. if the axis passes through a point at a distance from the centre equal to half the radius of the disc?
Given : Mass of disc = M = 0.5 kg, Radius of disc = R = 10 cm = 0.1 m
Solution:
Moment of inertia about a transverse axis passing through its centre is given by
I = MR2/2 = 0.5 x (0.1)2/2 = 0.25 x 0.25 = 0.0025 kgm2 = 2.5 x 10-3 kg m2
By parallel axes theorem

Ans: M.I. about the axis passes through a point at a distance from the centre equal to half the radius of the disc is 3.75 x 10-3 kg m2
Example – 07:
Calculate the M. I. of a solid brass sphere of radius 12 cm about a tangent to the sphere. Density of brass = 8500 kg/m3
Given: Radius of sphere = R = 12 cm = 0.12 m, density = r = 8500 kg/m3
Solution:
Moment of inertia of a solid sphere about its tangent is given by

Example – 08:
A solid sphere has a radius ‘R’. If its radius of gyration of this sphere about its diameter is √2/5R. show that the radius of gyration about the tangential axis of rotation is √7/5R.
Solution:
By parallel axes theorem

Example – 09:
If the radius of a solid sphere is doubled by keeping its mass constant, compare the moment of inertia about any diameter.
Given: R2 = 2R1
To Find: Ratio of M.I. = I1/I2 =?
Solution:
Moment of inertia of a solid sphere about its diameter is given by

Ans: The ratio of initial M.I. to the Final M.I. is 1:4
Example – 10:
A solid cylinder of uniform density of radius 2 cm has a mass of 50 g. If its length is 10 cm, calculate the moment of inertia about i) its own axis of rotation passing through its centre ii) an axis passing through its centre and perpendicular to the length.
Given: Mass of cylinder = M = 50 g = 0.05 Kg, Radius of cylinder = R = 2 cm = 0.02 m, length of cylinder = l = 10 cm = 0.1 m
To Find: Moment Of Inertia =?
Solution:
Moment of inertia of the cylinder about its own axis passing through its centre is given by
I = MR2/2 = 0.05 x (0.02)2/2 = 0.05 x 0.0004/2 = 10-5 kgm2
Moment of inertia of the cylinder about an axis passing through its centre and perpendicular to the length

Ans: Moment of inertia of the cylinder about its own axis passing through its centre is 10-5 kgm2. Moment of inertia of the cylinder about an axis passing through its centre and perpendicular to the length is 4.67 x 10-5 kgm2
Example – 11:
A solid sphere of diameter 25 cm and mass 25 kg rotates about an axis through its centre. Calculate its moment of inertia if its angular velocity changes from 2 rad/s to 12 rad/s in 5 seconds. Also, calculate torque applied.
Given: Diameter of sphere = 25 cm, Radius of sphere = R = 25/2 = 12.5 cm = 0.125 m, Mass of sphere = M = 25 kg, Initial angular speed ω1 = 2 rad/s, final angular speed = ω2 = 12 rad/s, time = t = 5 seconds.
To Find: Moment of inertia = I =? and torque = τ = ?
Solution:
Moment of inertia of a solid sphere about its diameter by

Ans: Moment of inertia of sphere is 0.1562 kg m2 and torque applied is 0.3124 Nm
Example -12:
A circular disc of mass 10 kg and radius 0.2 m is set into rotation about an axis passing through its centre and perpendicular to its plane by applying torque 10 Nm. Calculate the angular velocity of the disc at the end of 6 s from rest.
Given: Mass of disc = M = 10 kg, Radius of Disc = R = 0.2 m, Torque applied = t = 10 Nm, Initial angular speed w1 = 0 rad/s, time = t = 6 s.
To Find: final angular speed = ω2 =?
Solution:
Moment of inertia of disc about an axis passing through its centre and perpendicular to its plane is given by

Ans: Final angular speed is 300 rad/s
Example – 13:
A torque of 400 Nm acting on a body of mass 40 kg produces an angular acceleration of 20 rad/s2. Calculate the moment of inertia and radius of gyration of the body.
Given: Torque acting = τ = 400 Nm, Mass = M = 40 kg, angular acceleration = α = 20 rad/s2.
To Find: Moment of Inertia =?, Radius of gyration =?
Solution:
Torque acting on body is given by
τ = I α
I = τ/α = 400/20 = 20 kg m2.
Now the moment of inertia is given by
I = MK2
K2 = I/M = 20/40 = 0.5
K = √50
K = 0.707 m
Ans: The moment of inertia is 20 kg m2 and the radius of gyration is 0.707 m
Example – 14:
The M.I. of a uniform circular disc about an axis passing through its centre and perpendicular to its plane is ½ MR2. Find the distance of a parallel axis from the centre of mass about which the M.I. of the disc is MR2. Radius of disc = √2 cm.
Solution:
By parallel axes theorem

Ans: The distance of the axis is 1 cm
Example – 15:
A disc has a radius of gyration of 0.02 m when rotating about an axis passing through its centre and at right angles to its plane. What would be its radius of gyration when rotating about an axis coincident with a diameter of its face?
Given: Radius of gyration = K = 0.02 m for axis passing through centre.
To Find: Radius of gyration = K = ? for axis passing through diametre
Solution:
The M.I. in the first Case


Ans: The radius of gyration is 1.414 x 10-2 m
Example = 16:
Radius of gyration of a body about an axis at a distance of 0.12 m from its centre of mass is 0.13 m. Find its radius of gyration about a parallel axis through the centre of mass.
Given: Distance between axes = h = 0.12 m, radius of gyration = K = 0.13 m
To Find: Radius of gyration = K = ? for axis passing through centre.
Solution:

Ans: Radius of gyration is 0.05 m for axis passing through centre.
Previous Topic: Applications of Parallel and Perpendicular Axes
Next Topic: The Concept of Angular Momentum
2 replies on “Numerical Problems on Moment of Inertia and Radius of Gyration”
I like your arrangement of notes
I like your problems