Stresses and Strains in Compound Wires

Science > Physics > Elasticity > Stresses and Strains in Compound Wires

Problem – 1:

For two wires of the same material, both the radii and lengths are in the ratio 1:2. What should be the ratio of stretching forces on the wires if equal extensions are to be produced in the two?

Given: Ratio of radii = r₁ / r₂ = 1/2, Ratio of length = L₁ / L₂ = 1/2, Extension equal l₁ = l₂ hence l₁ / l₂ = 1, Material is same hence ratio of Young’s moduli Y₁ / Y₂ = 1,

To Find: Ratio of stretching force = F₁ / F₂ =?

Solution:

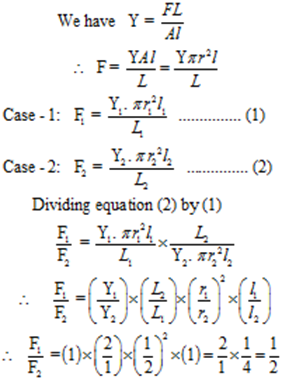
Ans: The ratio of stretching forces is 1:2.

Problem – 2:

Two wires of different material, but of the same cross-section and length are stretched by the same force. Find the ratio of Young’s moduli are of their material if the elongations produced in them are in the ratio 3:1.

Given: Same Cross-section, hence the ratio of area = A₁ /A₂ = 1, Lengths are same hence the ratio of length = L₁ / L₂ = 1, Same stretching force hence F₁ / F₂ = 1, Ratio of elongation l₁ / l₂ = 3:1,

To Find: Ratio of Young’s moduli = Y₁ / Y₂ =?

Solution:

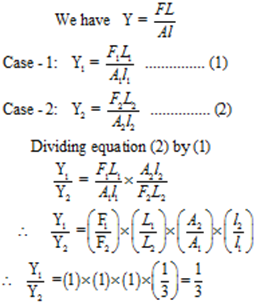
Ans: The ratio of Young’s moduli is 1:3.

Problem – 3:

Two wires are of the same material. Wire 1 if four times longer than the wire 2 but wire 1 has a diameter double that of wire 2. Compare stresses and elongations produced in the wires when under the same load.

Given: Material is same hence ratio of Young’s moduli Y₁ / Y₂ = 1, Length L₁ = 4 L₂ hence L₁ / L₂ = 4, Diameter d₁ = 2 d₂ hence d₁/d₂ = 2, hence ratio of radii = r₁/r₂ = 2, Load is same F₁ / F₂ = 1

To Find: Ratio of stresses =? Ratio of elongations =?

Solution:

To find the ratio of stresses

To find ratio of elongations

Ans: The ratio of stresses is 1:4

The ratio of elongation is 1:1. Hence elongations are equal

Example – 4:

Two wires of the same material have lengths in the ratio 2:1 and diameters are in the ratio 2:1 Find the ratio of extensions produced in the wires when the stretching forces acting on them are in the ratio 2:1

Given: Material is same hence ratio of Young’s  moduli Y₁ / Y₂ = 1, Ratio of lengths = 2: 1 i.e.  L₁ / L₂ = 2, Ratio of diameters = 2:1 hence d₁/d₂ = 2, hence ratio of radii = r₁/r₂ = 2, Load is same F₁ / F₂ = 2:1

To Find: Ratio of extensions =?

Solution:

Ans: The ratio of extension is 1: 1.

Hence the extensions in two wires are equal

Problems Based on Compound wire:

Example – 5:

A brass wire (Y = 11 × 10¹⁰ N/m²) and a steel wire (22 × 10¹⁰ N/m²) of the same length and cross-section are joined end to end. The composite wire is hung from a rigid support and weight is suspended from the free end. Find the extension in each wire if the increase in the length of the composite wire is 0.279 cm.

Given: Young’s modulus for brass Y_b = 11 × 10¹⁰ N/m², Young’s modulus for steel Y_s = 22 × 10¹⁰ N/m², Lengths of wire are same i.e L_b / L_s = 1, Crosssection are same i.e. A_b/A_s = 1, Load is same F_b / F_s = 1, Total extension in composite wire = l_b + l_s = 0.279 cm

To Find: extension in brass wire and steel wire =?

Solution:

l_b =  2 l_s

l_b + l_s = 0.279 cm

∴ 2 l_s + l_s = 0.279 cm

∴ 3 l_s = 0.279 cm

∴ l_s  = 0.093 cm

Now l_b = 2 l_s = 2 × 0.093 = 0.186 cm

Ans: Extension in brass wire = 0.186 cm and

extension in steel wire = 0.o93 cm

Example – 6:

A uniform brass wire (Y = 10 × 10¹⁰ N/m²) and a uniform steel wire (Y = 20 × 10¹⁰ N/m²) each of length 3.14 m and diameter 2 × 10^-3 m are joined end to end to form a composite wire is hung from a rigid support and a load suspended from the free end. If the increase in the length of the composite wire is 6 × 10^-3 m, find the increase in the length of each wire.

Given: Young’s modulus for brass Y_b = 10 × 10¹⁰ N/m², Young’s modulus for steel Y_s = 20 × 10¹⁰ N/m², Lengths of wire are same each 3.14 m i.e L_b / L_s = 1, Diameter is same each 2 × 10^-3 m, Hence cross-section are same i.e. A_b/A_s = 1, Load is same F_b / F_s = 1, Total extension in composite wire =  l_b + l_s = 6 × 10^-3 m

To Find: extension in brass wire and steel wire =?

Solution:

l_b =  2 l_s

l_b + l_s = 6 × 10^-3 m = 6 mm

∴ 2 l_s + l_s = 6 mm

∴ 3 l_s = 6 mm

∴ l_s = 2 mm

Now l_b = 2 l_s = 2 × 2 = 4 mm

Ans: Extension in brass wire = 4 mm and

extension in steel wire = 2 mm

Example – 7:

A light rod 1 m long is suspended horizontally by two wires of the same length and of the same cross-section but of different materials. The Young’s modulus of material of one wire is 30 x 1010N/m2 and that of the other is 20 x 1010N/m2. At what point should a weight W be hung from the rod so that it still remains horizontal? Ans: (0.4 m from the first wire)

Example – 8:

A weightless rod 105 cm long is suspended horizontally by two wires P and Q of equal length. The crosssection of P is 1 mm2 and that of Q is 2 mm2. From what point on the rod should a weight be suspended in order to produce equal strains in P and Q? Yp= 2 x 1011N/m2; YQ = 1011 N/m2.          Ans: (Midpoint)

Example – 9:

A brass wire of length 5 m and of sectional area 1 mm2 is hung from a rigid support with a brass weight of volume 1000 cc hanging from the other end. Find the decrease in length of the wire when the brass weight is completely immersed in water. Y = 1011N/m2. Take g = 10 m/s2. Density of brass = 8400 kg/m3 and of water = 1000 kg/m3. Ans: (0.5 mm)

Previous Topic: Problems on Poisson’s Ratio

Next Topic: Behaviour of Wire of Ductile Material Under Increasing Load

Science > Physics > Elasticity > Stresses and Strains in Compound Wires