Vector Algebra

Science > Physics > Scalars and Vectors > Vector Algebra

Resultant of Vectors:

A resultant vector is defined as a single vector whose effect is the same as the combined effect of two or more vectors.

Notes:

• The two vectors to be added should have the same nature. i.e. force can be added to force and velocity can be added to velocity, but the force cannot be added to the velocity.
• The two scalars to be added should have the same nature. i.e. mass can be added to mass and time can be added to time, but the mass cannot be added to the time.
• Scalar and vectors can never be added.

Composition of Vectors:

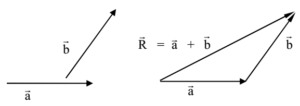
Triangle Law of Vector Addition:

Statement: 

When two vectors which are to be added taken in order are represented in direction and magnitude by two sides of a triangle then the third side taken in opposite order represents the resultant completely i.e. in direction and magnitude.

Procedure (Explanation):

• Consider two vectors which are to be added as shown. There resultant is found as follows.
• The first vector is drawn with a suitable scale and in the given direction
• Then from the head of the first vector, the second vector is drawn with the same scale and in the same direction of the second vector. Thus the tail of the second vector lies at the head of the first vector.
• Then the vector joining the tail of the first vector and the head of the second vector represents the resultant completely i.e. in the direction and magnitude.

Diagram :

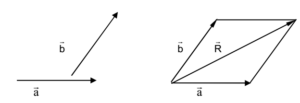
Parallelogram Law of Vector Addition:

Statement: 

If two vectors are represented in direction and magnitude by two adjacent sides of parallelogram then the resultant vector is given in magnitude and direction by the diagonal of the parallelogram starting from the common point of the adjacent sides.

Procedure (Explanation)

• Consider two vectors which are to be added as shown. There resultant is found as follows.
• The first vector is drawn with a suitable scale and in the given direction
• Then from the tail of the first vector, the second vector is drawn with the same scale and in the same direction of the second vector. Thus the tail of the second vector lies at the tail of the first vector.
• A parallelogram is completed by drawing lines parallel to vectors and  through the heads of vectors   and
• Then the diagonal passing through common tail represents the resultant completely, i e. in the direction and the magnitude.

Diagram:

Polygon Law of Vector Addition:

Statement: 

If a number of vectors are represented, in magnitude and direction, by the sides of an incomplete polygon taken in order, then their resultant is denoted by the closing side of the polygon in magnitude and direction, taken in the opposite order.

Procedure (Explanation):

• Consider a number of vectors which are to be added as shown. There resultant is found as follows.
• The first vector is drawn with a suitable scale and in a given direction.
• Then from the head of the first vector, the second vector is drawn with the same scale and in the same direction of the second vector. Thus every next vector should be drawn from the head of the previous vector and in its direction.
• Then the vector joining the tail of the first vector and the head of the last vector represents the resultant completely i.e. in the direction and magnitude.

Diagram:

Analytical Method to Find the Resultant of Two Vectors:

Let P and Q be the two vectors which are combined into a single resultant. Draw OA and OB to represent the vectors  P and Q  respectively to a suitable scale. The parallelogram OACB is constructed and the diagonal OC is drawn.

To find the magnitude of R

OA is produced and CD perpendicular to produced OA is drawn. In the Δ OCD

OC² = OD² + CD²

∴ OC² = (OA + AD)² + CD²

∴     OC² = OA² + 2 OA.AD + AD²  + CD²  ——–(1)

In the Δ ACD, AD² + CD²  = AC²

Substituting this in equation (1)

∴ OC²  = OA² + 2 OA.AD + AC² ———–(2)

If θ is the angle between the two vectors , then ∠ AOB =  θ,

But ∠ DAC = ∠ AOB = θ

In the Δ ACD,   AD = AC cos θ

Substituting this value in equation (2)

OC² = OA² + 2 OA.AC cos θ + AC²

But OC = R, OA = P, and AC = OB = Q

R² = P² + 2 P.Q cos θ + Q²

Using this relation the magnitude of the resultant can be determined.

To find the direction of  R :

Let α be the angle made by the resultant with vector P

Using this relation the direction of the resultant can be determined.

Special cases:

Case – I: When the two vectors are in the same direction, then θ = 0^o and cos 0^o = 1, we have

Thus when the two vectors are in the same direction the magnitude of the resultant is the sum of the magnitudes of the two vectors. The direction of the resultant is the same as the two vectors.

Case – II: When the two vectors are in the opposite direction then θ = 180^o and cos 180^o = – 1, we have

Thus when the two vectors are in the opposite direction the magnitude of the resultant is the difference of magnitude of the two vectors. The direction of the resultant is the same as the vector having a larger magnitude.

Case – III: When the two vectors are perpendicular to each other then θ = 90^o and cos 90^o = – 1, we have

Thus when the two vectors are perpendicular to each other, then the magnitude of the resultant of the two vectors is given by the above expression. The direction of the resultant is obtained using
the relation.

Characteristics of Vector Addition:

• Vector addition is commutative. i.e. A + B = B + A
• Vector addition is associative. i.e. (A + B) + C = A + (B + C)
• Their exists an additive identity of the vector. i.e. Zero vector is additive identity. If  is any vector and  is a zero vector, then Ā + ō = ō  + Ā  = Ā .
• There exists an additive inverse of a vector i.e. if Ā is any vector then there exists a vector – Ā  such that Ā + (-Ā) = 0.

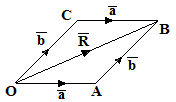
Vector Addition Obeys Commutative Law:

Consider two vectors a and b  which are to be added together,

Let us represent vector a and vector b by sides OA and AB of parallelogram OABC respectively.

In Triangle OAB, by the triangle law of vector addition

a  +  b  = R   ………… (1)

In Triangle OCB, by the triangle law of vector addition

b  +  a  = R   ………… (2)

From equations (1) and (2)

a  +  b  =  b  +  a

Thus vector addition is commutative. This law is known as the commutative law of vector addition.

Vector Addition Obeys Associative Law:

Consider three vectors a, b  and c  which are to be added together,

Vectors a, b and c are represented by sides OA, AB, and BC of the polygon

Applying polygon law of vector addition the resultant  R is found

Applying triangle law of vector addition to the Δ OAB, we have

  a  +  b  = P   ………… (1)

Applying triangle law of vector addition to the Δ OBC, we have

 P  +  c  = R    ………… (2)

From (1) and (2) we have

R = ( a  + b ) + c   ……….. (3)

Now, Applying triangle law of vector addition to the Δ ABC, we have

 b  +  c  = Q   ………… (4)

Now, Applying the triangle law of vector addition to the Δ OAC, we have

 a  +  Q = R    ………… (5)

From (4) and (5) we have

R =  a  + ( b  + c )  ……….. (3)

From (3) and (6)

 ( a  + b ) + c  =  a  + ( b  + c )

Thus vector addition is associative. This law is known as the associative law of vector addition.

Notes:

• When two vectors having the same magnitude are acting on a body in opposite directions, then their resultant vector is zero.
• Two vectors of different magnitudes cannot give zero resultant vector.
• Three vectors of different or same magnitudes can give zero resultant vector if they are collinear. In such case, if they are represented in direction and magnitude taken in order (one after another) then, they form a closed triangle.

 Subtraction of Vectors:

Subtraction of vectors can be treated as the addition of a vector and a negative vector.

Procedure (Explanation):

• Consider two vectors which are to be subtracted as shown. There resultant is found as follows.
• The first vector is drawn with proper scale and in a given direction
• Then from the head of the first vector, a vector is drawn with the same scale and in the opposite direction of the second vector.
• Then the vector joining the tail of the first vector and head of the second vector represents the resultant completely i.e. in direction and magnitude.

Diagram:

Multiplication of Vector by Scalar:

Let m be any scalar and  Ā be any vector then the product mĀ or Ām of the vector and the scalar m is a vector whose magnitude is |m| times that of  Ā and the support is the same or parallel to that of Ā  and the sense is the same or opposite to that of  Ā.

Notes:

• If m > 0 then mĀ is a vector whose magnitude is m|Ā| and whose direction is the same as that of Ā.
• If m < 0 then mĀ is a vector whose magnitude is m|Ā| and whose direction is opposite of Ā.
• If m = 0 then mĀ =  0  = Ām
• If A, B are collinear or parallel vectors, then B = mA, where m is some scalar. Thus B can be expressed as a scalar multiple of A and vice versa.

Properties of Scalar Multiplication:

• If A, B are vectors and m, n are scalars, then
• m(A + B) = mA + mB
• (m + n) A  = mA + nA
• m(nA) (m n)A

Multiplication of Vector by a real Number:

A multiplication of a vector by a real number results in a vector of the same nature but a different magnitude. The magnitude of the resulting vector is real number times the original vector and has the same direction as the original vector. Example: 4(5 km h^-1 east) ≡ (20 km h^-1 east)

In this case, the velocity vector (5 km h^-1 east) is multiplied by 4, the resultant vector (20 km h^-1 east) is also a velocity vector (same nature)  directed towards the east (same direction).

Multiplication of Vector by a Scalar:

A multiplication of a vector by scalar results in a vector of the different nature. The direction of the resultant is the same as the original vector. Example: 4 h (5 km h^-1 east) ≡ (20 km east)

In this case, the velocity vector (5 km h^-1 east) is multiplied by 4 h (scalar), the resultant vector (20 km east) is a displacement vector (different nature)  directed towards the east (same direction).

Example – 01:

Two forces of magnitude 5 N each are inclined at 60° each other act on the body. Find the resultant of the two forces.

Given: F₁ = 5N, F₂ = 5 N, θ = 60°

To Find: Resultant R = ?, α = ?

Solution:

We have R² = F₁² + F₂² = 2 F₁ F₂ cos θ

∴ R² = 5² + 5² + 2 × 5 × 5 × cos 60°

∴ R² = 25 + 25 + 50 × 0.5 = 25 + 25 + 25 = 75

∴ R = √75

∴ R = 8.66 N

Ans: Magnitude of resultant is 8.66 N and it makes an angle of 30° with force F₁.

Example – 02:

Two forces of magnitude 3 N  and 2N are inclined at 30° to each other act on the body. Find the resultant of the two forces.

Given: F₁ = 3N, F₂ = 2 N, θ = 30°

To Find: Resultant R = ?, α = ?

Solution:

We have R² = F₁² + F₂² = 2 F₁ F₂ cos θ

∴ R² = 3² + 2² + 2 ×3 × 2 × cos 30°

∴ R² = 9 + 4 + 12 ×0.866 = 13 + 10.392 = 23.392

∴ R = √23.392

∴ R = 4.837 N

Ans: Magnitude of resultant is 4.837 N and it makes an angle of 11°56′ with force 3 N force

Previous Topic: Concept of Scalars and Vectors

Next Topic: Scalar Product and Vector Product

Science > Physics > Scalars and Vectors > Vector Algebra