Science > Physics > Wave Motion > Speed of Longitudinal Waves
In this article, we shall study to solve problems to find speed of longitudinal waves in fluids, solids, and rods.
Expression for velocity of longitudinal wave in a fluid using dimensional analysis:
The velocity (v) of longitudinal wave through a fluid is found to depend on the bulk modulus of elasticity (K) of the fluid and the density (ρ) of the fluid.
v α Kx ……….. (1)
v α ρ y ……….. (2)
From above relations we have
v α Kx ρ y
∴ v = CKx ρ y ……….. (3)
By principle of homogeneity of dimensions
[L.H.S.] = [R.H.S.]
∴ [v] = [C][K]x[ρ]y
∴ [M0L1T-1] = [M0L0T0][ M1L-1T-2]x[M1L-3T0]y
∴ [M0L1T-1] = [M0L0T0][ MxL-xT-2x] [MyL-3yT0]
∴ [M0L1T-1] = [Mx + yL-x-3yT-2x]
∴ – 2x = -1 hence x = ½
∴ x + y = 0
∴ 1/2 + y = 0
∴ y = -1/2
Substituting values of x and y in equation (3)
v = CK1/2 ρ -1/2
Squaring both sides
v2 = C2K ρ -1
Experimentally it is found that C = 1
∴ v2 = K/ ρ
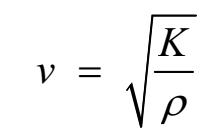
This is an expression for velocity of longitudinal wave in a fluid.
Expression for velocity of longitudinal wave in a solid:
The speed of longitudinal wave (v) in a solid having bulk modulus K, modulus of rigidity η, and density ρ is given by
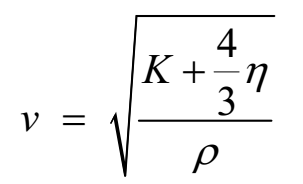
The quantity K + (4/3) η is called elongation elasticity.
Expression for velocity of longitudinal wave in a solid rod:
Solid rod is a thin compared to its length, hence its sideway expansion is negligible. In this case we have to consider longitudinal strain only. Thus, corresponding modulus of elasticity is Young’s modulus of elasticity (Y). The speed of longitudinal wave (v) in a solid rod having Young’s modulus of elasticity Y and density ρ is given by
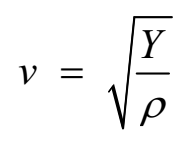
Numerical Problems:
Example 01:
At pressure of 105 N m-2, the volumetric strain in water is 5 x 10-5. If the density of water is 103 kg m-3, find the speed of sound in water.
Given: Pressure = Volumetric stress = P = 105 N m-2, Volumetric strain = 5 x 10-5,Density of water = ρ = 103 kg m-3.
To Find: Velocity of the wave = v =?
Solution:
Bulk modulus = K = Volumetric stree/Volumetric strain
∴ K = 105/5 x 10-5 = 2 x 109 N m-2
Speed of longitudinal wave in a fluid is given by

∴ v = 1.414 x 103 m s-1
Ans: The speed of sound wave in water is 1.414 x 103 m s-1.
Example 02:
An increase in pressure of 100 kPa causes a certain volume of water to decrease by 0.005% of its original volume. Calculate the speed of sound (compressional waves) in water.
Given: Pressure = Volumetric stress = P = 100 kPa = 100 x 103 Pa, Volumetric strain = 0.005 % = 0.005/100 = 5 x 10-5,Density of water = ρ = 103 kg m-3.
To Find: Velocity of the wave = v =?
Solution:
Bulk modulus = K = Volumetric stree/Volumetric strain
∴ K = 100 x 103/5 x 10-5 = 2 x 109 N m-2
Speed of longitudinal wave in a fluid is given by

∴ v = 1.414 x 103 m s-1
Ans: The speed of sound wave in water is 1.414 x 103 m s-1.
Example 03:
The speed of sound in a liquid of density 103 kg m-3 is 1500 m s-1, Find the bulk modulus of liquid.
Given: Density of liquid = ρ = 103 kg m-3, Speed of sound = v = 1500 m s-1.
To Find: Bulk modulus of elasticity = K =?
Solution:
Speed of longitudinal wave in a fluid is given by

∴ K = (1500)2 x 103
∴ K = 2.25 x 109 N m-2
Ans: The bulk modulus of elasticity 2.25 x 109 N m-2.
Example 04:
The longitudinal waves starting from ship return from bottom of the sea to ship after 2.64 s. If bulk modulus of water is 220 kg mm-2 and density 1.1 x 103 m s-1, Calculate the depth of sea.
Given: Bulk modulus of elasticity = K = 220 kg mm-2 = 220 x 9.8 x (10-3)-2 N m-2 = 2.156 x 109 N m-2, Density of sea water = ρ = 1.1 x 103 kg m-3.
To Find: Depth of sea =?
Solution:
Speed of longitudinal wave in a fluid is given by

∴ v = 1.4 x 103 m s-1
Time taken by wave to reach from ship to bottom of sea
= t = 2.64/2 = 1.32 s
Depth of sea: Speed of sound in sea x t
∴ Depth of sea = 1.4 x 103 x 1.32 = 1.848 x 103 m
Ans: The depth of sea is 1848 m.
Example 05:
Calculate the speed of sound in a steel rod whose Young’s modulus Y = 2 × 1011 N m-2 and ρ = 7800 kg m-3.
Given: Young’s modulus of elasticity = Y = 2 x 1011 N m-2, Density of steel = ρ = 7800 kg m-3.
To Find: Velocity of the wave = v =?
Solution:
Speed of longitudinal wave in a metal rod is given by

∴ v = 5.06 x 103 m s-1
Ans: The speed of sound wave in steel rod is 5.06 x 103 m s-1.
Example 06:
Longitudinal waves are produced in a certain rod of density 2600 kg m-3 and Young’s modulus 6.5 × 1010 Nm−2. Find the speed of sound in the given rod.
Given: Young’s modulus of elasticity = Y = 6.5 x 1011 N m-2, Density of steel = ρ = 2600 kg m-3.
To Find: Velocity of the wave = v =?
Solution:
Speed of longitudinal wave in a metal rod is given by

∴ v = 5 x 103 m s-1
Ans: The speed of sound wave in steel rod is 5 x 103 m s-1.
Example 07:
Calculate the speed of sound in a metal rod whose Young’s modulus Y = 2.9 × 1011 N m-2 and ρ = 8 x 103 kg m-3.
Given: Young’s modulus of elasticity = Y = 2.9 x 1011 N m-2, Density of steel = ρ = 8 x 103 kg m-3.
To Find: Velocity of the wave = v =?
Solution:
Speed of longitudinal wave in a metal rod is given by

∴ v = 6.02 x 103 m s-1
Ans: The speed of sound wave in the rod is 6.02 x 103 m s-1.
Example 08:
For aluminium rod bulk modulus of elasticity and the modulus of rigidity are 7.5 x 1010 N m-2 and 2.1 x 1010 N m-2. If the density of aluminium is 2.7 x 103 kg m-3, find the speed of longitudinal waves in aluminium.
Given: Bulk modulus of elasticity = K = 7.5 x 1010 N m-2, Modulus of rigidity = η = 2.1 x 1010 N m-2, Density = ρ = 2.7 x 103 kg m-3.
To Find: Speed of longitudinal wave = v=?
Solution:
Speed of longitudinal wave in a solid is given by

∴ v = 6.18 x 103 m s-1
Ans: The speed of longitudinal waves in aluminium is 6.18 x 103 m s-1.