Speed of Transverse Waves

Science > Physics > Wave Motion > Speed of Transverse Waves

In this article, we shall study to solve problems to find speed of transverse wave in a stretched string and a solid.

Expression for velocity of transverse wave on a stretched string using dimensional analysis:

The velocity (v) of transverse wave on a stretched string is found to depend on the tension (T) in the string and linear mass density (m) of the string.

v α T^x ……….. (1)

v α m^y ……….. (2)

From above relations we have

v α T^xm^y

∴ v = kT^xm^y ……….. (3)

By principle of homogeneity of dimensions

[L.H.S.] = [R.H.S.]

∴ [v] = [k][T]^x[m]^y

∴ [M⁰L¹T^-1] = [M⁰L⁰T⁰][ M¹L¹T^-2]^x[M¹L^-1T⁰]^y

∴ [M⁰L¹T^-1] = [M⁰L⁰T⁰][ M^xL^xT^-2x] [M^yL^-yT⁰]

∴ [M⁰L¹T^-1] = [M^{x + y}L^{x – y}T^-2x]

∴ – 2x = -1 hence x = 1/2

∴ x + y = 0

∴ 1/2 + y = 0

∴ y = -1/2

Substituting values of x and y in equation (3)

v = kT^1/2m^-1/2

Squaring both sides

v² = k²Tm^-1

Experimentally it is found that k = 1

∴ v² = T/m

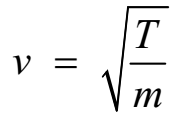
This is an expression for velocity of transverse wave on a stretched string.

Expression for velocity of transverse wave in a solid using dimensional analysis:

The velocity (v) of transverse wave in solid is found to depend on the Elastic modulus of rigidity of the solid medium (E) and the density of medium (ρ).

v α η^x ……….. (1)

v α ρ ^y ……….. (2)

From above relations we have

v α η^x ρ ^y

∴ v = kη^x ρ ^y ……….. (3)

By principle of homogeneity of dimensions

[L.H.S.] = [R.H.S.]

∴ [v] = [k][η]^x[ρ]^y

∴ [M⁰L¹T^-1] = [M⁰L⁰T⁰][ M¹L^-1T^-2]^x[M¹L^-3T⁰]^y

∴ [M⁰L¹T^-1] = [M⁰L⁰T⁰][ M^xL^-xT^-2x] [M^yL^-3yT⁰]

∴ [M⁰L¹T^-1] = [M^{x + y}L^-x-3yT^-2x]

∴ – 2x = -1 hence x = ½

∴ x + y = 0

∴ 1/2 + y = 0

∴ y = -1/2

Substituting values of x and y in equation (3)

v = kη^1/2 ρ ^-1/2

Squaring both sides

v² = k²η ρ ^-1

Experimentally it is found that k = 1

∴ v² = η/ ρ

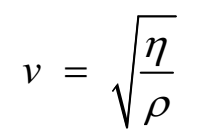
This is an expression for velocity of transverse wave in a solid.

Numerical Problems:

Example 01:

A steel wire 0.72 m long has a mass of 5.0 x 10^-3 kg. If the wire is under tension of 60 N, what is the speed of transverse wave in the string.

Given: Length o wire = L = 0.72 m, Mass of wire = M = 5.0 x 10^-3 kg, Tension in wire = T = 60 N.

To Find: Velocity of the wave = v =?

Solution:

Linear mass density = m = M/L

m = 5 x 10^-3/0.72 = 6.9 x 10^-3 kg m^-1

Velocity of wave in the wire in a stretched string is given by

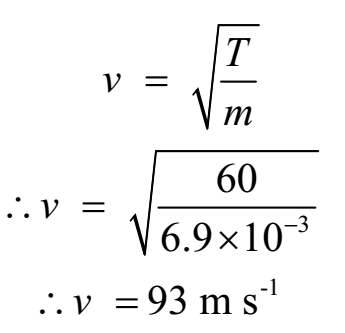
Ans: The speed of transverse wave in the string is 93 m s^-1.

Example 02:

A steel wire 70 cm long has a mass of 7 g = 7 x 10^-3 kg. If the wire is under tension of 100 N, what is the speed of transverse wave in the string.

Given: Length o wire = L = 70 cm = 0.70 m, Mass of wire = M = 7 g = 7 x 10^-3 kg, Tension in wire = T = 100 N.

To Find: Velocity of the wave = v =?

Solution:

Linear mass density = m = M/L

m = 7 x 10^-3/0.70 = 10^-2 kg m^-1

Velocity of wave in the wire in a stretched string is given by

Ans: The speed of transverse wave in the string is 100 m s^-1.

Example 03:

A thin wire one metre long, weighing 0.002 kg, is stretched by a weight of 9 kg. Find the velocity of transverse waves set up on the wire when plucked. What is the frequency of the fundamental note emitted by the wire? What is the frequency of the second harmonic?

Given: Vibrating length of wire = l = 1 m, Mass of the wire = M = 0.002 kg, Tension in wire = T = 9 kg-wt = 9 × 9.8 N,

To Find: Velocity of wave = v =? Frequency of fundamental mode =?, Frequency of second harmonic = ?

Solution:

Linear density = m = M/l = 0.002/1

∴ m = 0.002 kg m^-1

Velocity of wave in the wire in a stretched string is given by

Ans: The velocity of the wave = 210 m s^-1.

Example 04:

A wave pulse is travelling on a string of linear mass density 1.0 g cm^-1 under a tension of 1 kg wt. Calculate the time taken by a pulse to travel a distance of 50 cm on the string. Given g = 10 m s^-2.

Given: Linear mass density = m = 1.0 g cm^-1 = 1.0 (10^-3 kg) (10^-2 m)^-1 = 0.1 kg m^-1 , Tension = T = 1 kg wt = 1 x 10 N = 10 N, Distance = 50 cm = 0.5 m.

To Find: Time taken by pulse to travel 50 cm = t =?

Solution:

Velocity of wave in the wire in a stretched string is given by

Speed = Distance/Time

∴ Time = Distance/Speed = 0.5/10 = 0.05 s

Ans: The time taken by a pulse to travel a distance of 50 cm on the string is 0.05 s

Example 05:

The speed of a transverse wave in a stretched string is 348 m s^-1, when the tension in the string is 3.6 kg wt. Calculate the speed of the transverse wave on the same string, if the tension in the string is changed to 4.9 kg wt.

Given: Initial speed = v₁ = 348 m s^-1, Initial tension = T₁ = 3.6 kg wt, Final tension = T₂ = 4.9 kg wt.

To Find: Final speed = v₂ =?

Solution:

As string is same

Ans: The new speed of transverse wave is 406 m s^-1.

Example 06:

The speed of a transverse wave in a stretched string is 20.0 m s^-1, when the tension in the string is 6.00 N. If the speed of the transverse wave on the same string is 30.0 m s^-1, find the tension in the string.

Given: Initial speed = v₁ = 20.0 m s^-1, Initial tension = T₁ = 6.00 N, Final speed = v₂ = 30.0 m s^-1,

To Find: Final tension = T₂ =?

Solution:

As string is same

Ans: The new tension in the string is 13.5 N.

Example 07:

Calculate the velocity of transverse wave in a copper wire of cross-section 1 mm², under a tension produced by 1 kg wt. The density of copper is 8.93 g cm^-3.

Given: Area of cross-section = A = 1 mm2 = 1 x 10-6 m2, Tension = T = 1 kg wt = 1 x 9.8 N, Density of copper = ρ = 8.93 g cm^-3 = 8.93 x 10³ kg m^-3.

To Find: Velocity of wave = v =?

Solution:

Velocity of wave in the wire is given by

Ans: The velocity of the wave = 33.13 m s^-1.

Example 08:

In a sonometer experiment the density of the material of the wire used is 7.5 x 10³ kg m^-3. If the stress of the wire is 3.0 x 10⁸ N m^-2, find the speed of transverse wave in the wire.

Given: Density of material of wire = ρ = 7.5 x 10³ kg m^-3, Stress – 3.0 x 10⁸ N m^-2,

To Find: Sped of the wave = v =?

Solution:

Velocity of wave in the wire is given by

Ans: Speed of transverse wave is 200 m s^-1.

Example 09:

The diameter of an iron wire is 1.20 mm. If the speed of transverse wave be 50.0 m s^-1, what is the tension in the wire? The density of iron is 7.7 x 10³ kg m^-3.

Given: Diameter of wire = d = 1.20 mm = 1.20 x 10^-3 m, Speed of wave = v = 50.0 m s^-1, Density of iron = ρ = .7 x 103 kg m^-3.

To Find: Tension in the wire = T =?

Solution:

Example 10:

A copper wire is held at the two ends by rigid supports. At 30 ^oC the wire is just taut with negligible tension. Find the speed of transverse wave in the wire at 10 ^oC. Given α = 1.7 x 10^{-5 o}C^-1, Y = 1.4 x 10¹¹ N m^-2, = 9 x 10³ kg m^-3.

Solution:

∴ v = 72.72 m s^-1.

Ans: The speed of transverse wave is 72.72 m s^-1.

Example 11:

For aluminium the modulus of rigidity is 2.1 x 10¹⁰ N m^-2 and density 2.7 x 10³ kg m^-3. Find the speed of transverse wave in the medium.

Given: Modulus of rigidity = η = 2.1 x 10¹⁰ N m^-2, Density of aluminium = ρ = 2.7 x 10³ kg m^-3.

To Find: Velocity of wave = v =?

Solution:

Velocity of wave in solid is given by

∴ v = 2.7 x 10³ ms^-1

Ans: Speed of transverse wave in aluminium is 2.7 x 10³ ms^-1.