Science > Physics > Surface Tension > Concept of Surface Energy
In this article, we shall study the concept of surface energy, relation between the surface energy and surface tension.
A molecule on the surface of a liquid experiences a downward pull due to surface tension. If a molecule deep inside the liquid is to be lifted up towards the fine surface, as soon as it enters the surface film, work will have to be done to lift it further against the unbalanced downward forces of molecular attraction.
This work will be stored in the molecule as potential energy. This is true of every molecule on the surface film and surface film possesses a certain amount of potential energy. Thus the molecules in surface film possess extra energy. This energy is called as surface energy. Its S.I. unit is J and its dimensions are [L2M1T-2].
Relation Between Surface Tension and Surface Energy:
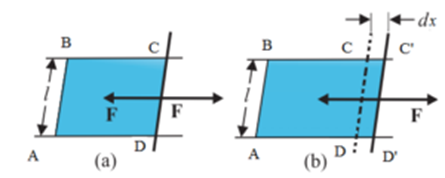
Consider a rectangular frame ABCD in which side CD is made of loose write and other three sides are fixed. The frame is immersed in a soap solution and taken out and held horizontally. A film of soap solution will be formed on the frame and it will at once try to shrink and pull the loose wire CD towards AB. If the length of loose wire CD is ‘l’ and the film is of finite thickness, therefore the film will be in contact with the wire both on the upper surface as well as along its lower surface. Hence the length of the wire in contact with the film is ‘ 2l ‘. The force acting on the wire is directed towards AB, per unit length of the contact line is surface tension (T). By definition of surface tension, we have
T = F / 2l
∴ F = T . 2 l … (1)
Imagine an external force is applied on CD which is equal and opposite to force F Let the wire at CD moves to C’D’ through small distance dx. Then the work done against the force of surface tension is given by
dW = F.dx … (2)
From equations (1) and (2),
dW = T.2l. dx
But, 2l . dx = dA = increase in Area of both the surface of the film.
∴ dW = T.dA
This work done is stored inside the films as potential energy dU.
∴ dU = T.dA
If, initially CD is very close to AB, initial energy and initial area of the film can be taken as zero and dU and dA can be treated as total energy and the total area of the film respectively.
∴ T = dU / dA
This expression indicates that surface tension is equal to surface energy per unit area of the surface film.
Numerical Problems:
Example -1:
A water film is formed between two straight parallel wires of 10 cm each with a separation of 0.1 cm. If the distance between the wires is increased by 0.1 cm, how much work is done? T = 0.072 N/m
Given: Length of wire= l = 10 cm = 10 × 10-2 m, Increase in width = 0.1 cm = 0.1 × 10-2 m, Surface tension = T = 0.072 N/m
To Find: Work done = W =?
Solution:
In this case, the film has two surfaces
dA = 2 (l × b) = 2 × 10 × 10-2 × 0.1 × 10-2 m
dA = 2 × 10-4 m2
Work done = Change in surface energy = T. dA
Ans: The work done = 0.072 × 2 × 10-4 = 1.44 × 10-5 J
Work done is 1.44 × 10-5 J
Example – 2:
A liquid film is formed in a rectangular frame one side of which is a light and thin movable wire of length 4 cm. The frame is held in a vertical plane with the movable wire in the downward position. Find what weight required to hold the movable wire in equilibrium. How much work is done if the film is stretched by pulling the movable wire downwards by 2 cm? T = 0.025 N/m.
Given: Length of wire= l = 4 cm = 4 × 10-2 m, displacement = dx = 2 cm = 2 × 10-2 m, Surface tension = T = 0.025 N/m.
To Find: Weight required = F =?, Work done = W = ?
Solution:
In case of wire, the water wets it from two sides,
Hence, the effective length = 2 l
We have, T = F / effective length
∴ F = T × effective length = T × 2 l
F = 0.025 × 2 × 4 × 10-2 = 0.002 N
In this case, the film has two surfaces
dA = 2 (l × dx) = 2 × 4 × 10-2 × 2 × 10-2 m
dA = 16 × 10-4 m2
Work done = Change in surface energy = T. dA
Work done = 0.025 × 16 × 10-4 = 4 × 10-5 J
Ans: The weight required is 0.002 N and work done is 4 × 10-5 J
Example – 3:
There is a soap film on a rectangular wire frame of area 4cm × 4 cm. If area of the frame is increased to 4cm x 5 cm, find work done in the process. Surface tension of soap film is 3 × 10-2 N/m.
Given: Initial area= A1 = 4cm × 4 cm = 16 cm2 = 16 × 10-4 m2, Final area= A2 = 4cm × 5 cm = 20 cm2 = 20 × 10-4 m2, Surface tension = T =3 × 10-2 N/m.
To Find: Work done = W =?
Solution:
In case of rectangular frame, the water wets it from two sides,
Hence, the change in area = dA = 2 (A2 – A1)
dA = 2 × (20 × 10-4 – 16 × 10-4)
∴ dA = 2 (A2 – A1) = 2 × 4 × 10-4 = 8 × 10-4 m2
Work done = Change in surface energy = T. dA
Work done = 3 × 10-2 × 8 × 10-4 = 2.4 × 10-5 J
Ans: The work done is 2.4 × 10-5 J
Example – 4:
Find the work done in blowing a soap bubble of radius 5 cm. S.T. of soap solution = 0.035 N/m.
Given: Radius of bubble = r = 5 cm = 5 × 10-2 m, Surface tension = T = 0.035 N/m
To Find: Work done = W =?
Solution:
In case of bubble it has two free surfaces
dA = 2 (4 π r²) = 8 π r²
Work done = Change in surface energy = T. dA = T × 8 π r²
∴ Work done = 0.035 × 8 × 3.142 × ( 5 × 10-2)2
∴ Work done = 0.035 × 8 × 3.142 × 25 × 10-4 = 2.2 × 10-3 J
Ans: The work done is 2.2 × 10-3 J
Example – 5:
Find the work done in blowing a soap bubble of radius 10 cm. S.T. of soap solution = 30 dyne/cm.
Given: Radius of bubble = r = 10 cm = 10 × 10-2 m, Surface tension = T =30 dyne/cm = 30 × 10-3 N/m.
To Find: Work done = W =?
Solution:
In case of bubble it has two free surfaces
dA = 2 (4 π r²) = 8 π r²
Work done = Change in surface energy = T. dA = T × 8 π r²
∴ Work done = 30 × 10-3 × 8 × 3.142 × (10 × 10-2)2
∴ Work done = 30 × 10-3 × 8 × 3.142 × 100 × 10-4 = 7.54 × 10-3 J
Ans: The work done is 7.54 × 10-3 J
Example – 6:
Calculate the work done in increasing the radius of a soap bubble in air from 1 cm to 2 cm. The surface tension of a soap solution is 30 dyne/cm.
Given: Initial radius of bubble = r1 = 1 cm = 1 × 10-2 m, Final radius of bubble = r2 = 2 cm = 2 × 10-2 m, Surface tension = T = 30 dyne/cm = 30 × 10-3 N/m.
To Find: Work done = W =?
Solution:
In case of bubble it has two free surfaces
dA = A2 – A1 = 2 (4 π r2²) – 2 (4 π r1²)
∴ dA = 8 π ( r2² – r1²) = 8 π ( (2 × 10-2)² – (1 × 10-2)²)
∴ dA = 8 π ( 4 × 10-4 – 1 × 10-4)
dA = 8 π × 3 × 10-4
Work done = Change in surface energy = T. dA
Work done = 30 × 10-3 × 8 π × 3 × 10-4
Work done = 30 × 10-3 × 8 × 3.142 × 3 × 10-4 = 2.262 × 10-4 J
Ans: The work done is 2.262 × 10-4 J
Example – 7:
The total energy of the free surface of a liquid drop is 2π times the surface tension of the liquid. What is the diameter of the drop? Assume all terms in S.I. unit.
Solution:
In case of liquid drop it has one free surfaces
dA = 4 π r²
Surface energy = T. dA = T × 4 π r²
∴ 2π T = T × 4 π r²
∴ 2 = 4 r²
∴ 0.5 = r²
∴ r = 0.707 m
Ans: The diameter = d = 2 r = 2 × 0.707 = 1.414 m
Problem – 8:
A soap bubble of radius 12 cm is blown. The surface tension of soap solution is 30 dynes/cm. Calculate the work done in blowing the soap bubble.
Given: Radius of bubble = r = 12 cm = 12 × 10-2 m, Surface tension = T =30 dyne/cm = 30 × 10-3 N/m.
To Find: Work done = W = ?
Solution:
In case of bubble it has two free surfaces
dA = 2 (4 π r²) = 8 π r²
Work done = Change in surface energy = T. dA = T × 8 π r²
∴ Work done = 30 × 10-3 × 8 × 3.142 × ( 12 × 10-2)2
∴ Work done = 30 × 10-3 × 8 × 3.142 × 144 × 10-4 = 0.01086J
Ans: The work done is 0.01086J
Problem – 9:
The energy of the free surface of liquid drop is 5π times the surface tension of the liquid. Find the diameter drop in c.g.s. System.
Solution:
In case of liquid drop, it has one free ssurface
dA = 4 π r²
Surface energy = T. dA = T × 4 π r²
∴ 5π T = T × 4 π r²
∴ 5 = 4 r²
∴ 1.25 = r²
∴ r = 1.12 cm
Ans: diameter = d = 2 r = 2 × 1.12 = 2.24 cm
Problem – 10:
The total free surface energy of a liquid drop is π √2 times the surface tension of the liquid. Calculate the diameter of the drop in S.I. unit.
Solution:
In case of liquid drop, it has one free ssurface
dA = 4 π r²
Surface energy = T. dA = T × 4 π r²
∴ π √2 T = T × 4 π r²
∴ 5√2 = 4 r²
∴ 5√2 / 4 = r²
∴ r = 1.33 m
Ans: The diameter = d = 2 r = 2 × 1.33 = 2.66 cm
Problem – 11:
Two soap bubbles have radii in the ratio 4:3. What is the ratio of work done to blow these bubbles?
Given: r1 / r2=4/3, Surface tension = T1 =T2 = T
To Find: W1 / W2 =?
Solution:
In case of bubble it has two free surfaces
dA = 2 (4 π r²) = 8 π r²
Work done = Change in surface energy = T. dA = T × 8 π r²
For First Bubble W1 = T1 × 8 π r1² …………. (1)
For second Bubble W2 = T2 × 8 π r2² …………. (2)
Dividing equation (1) by (2) we get
W1 / W2 = (T1 × 8 π r1² ) / (T2 × 8 π r2² )
W1 / W2 = (r1 / r2 )² = = (4/3 )² = 16/9
Ans: The ratio of work done to blow these bubbles is 16 : 9
Previous Topic: Numericl Problems on Surfce Tension
Next Topic: Numerical Problems on Change in Surface Energy
One reply on “Concept of Surface Energy”
This is the only place where I found about the origin of the relationship between surface tension and the work done. Thank you so much