Science > Physics > Magnetism > Torque Acting on Bar Magnet in Uniform Magnetic Field
In this article, we shall study the force acting on poles and torque action on bar magnet suspended in a uniform magnetic field.
Force Between Two Magnetic Poles (Inverse Square law):
If two poles of strengths m1 and m2 separated by a distance ‘r’ from each other in a vacuum, then the force between the two magnetic poles is given by
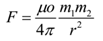
Problems on Inverse Square Law
Example – 01:
The force between two magnetic poles in the air is 9.604 mN. If one pole is ten times stronger than other, calculate the pole strength of each magnet. The distance between the poles of two magnets is 0.1 m.
Given: Force = F = 9.604 mN = 9.604 x 10-3 N, distance between poles = r = 0.1 m, Relation between pole strength m2 = 10 m1, μo/4π = 10-7 Wb/Am.
To Find: pole strengths = ?
Solution:
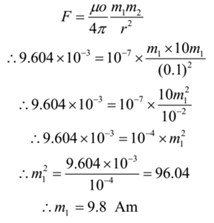
m2 = 10 m1 = 10 x 9.8 = 98 Am
Ans: The pole strengths of magnets are 9.8 Am and 98 Am.
Example – 02:
What is the force of repulsion between two magnetic poles of strengths 1.6 Am and 7.2 Am separated by a distance 0.06 m in a vacuum?
Given: pole strengths m1 = 1.6 Am and m2 = 7.2 Am, distance between poles = r = 0.06 m, μo/4π = 10-7 Wb/Am.
To Find: The force between poles = F = ?
Solution:
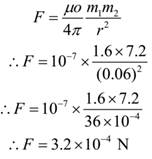
Ans: Force Between Poles is 3.2 x 10-4 N
Force Experienced by a Pole of Magnet in Uniform Magnetic Field:
If we try to break the bar magnet at the centre and separate the poles, new poles are formed at the broken ends. It means it is not possible for us to separate the poles and study them individually hence the magnetic circuit is studied in analogy with the electrical circuit. Analogous to the quantity of electrical field intensity we have similar quantity magnetic field intensity. It is also referred as magnetic induction. The electrical field intensity at a point is defined as the force experienced by a unit charge kept at that point.

By analogy, we can define magnetic induction at a point as the force experienced by a pole of unit strength kept at that point. Let the strength of the magnetic field be B.

Thus the N-pole is acted upon by a force of magnitude mB and the south pole is acted upon by a force of magnitude mB, in the opposite direction to that on the north pole.
Torque Acting on Bar Magnet in a Uniform Magnetic Field:
Let us consider a bar magnet of pole strength, ‘m’ and magnetic length ‘2l’ suspended in a magnetic field of induction B such that it is free to rotate about a transverse axis passing through its centre. Let θ be the angle between the axis of the bar magnet and the direction of the magnetic field.
The magnetic dipole moment of a bar magnet is given by
M = m . 2l …………… (1)
Now, each pole of the bar magnet is acted upon by a force whose magnitude is given by
F = mB …………… (2)

The force acting on the north pole is equal to the force acting on the south pole but they act in the opposite direction. Similarly, the lines of action of these two forces are different, Hence they form what is called a couple.
The magnitude of the couple or moment of force is given by
Torque ( τ ) = Force (F) . Perpendicular distance between the forces
∴ τ = F . SP
∴ τ = F . 2l sin θ ………………. (3)
From equations (2) and (3)
τ = m B . 2l sin θ
∴ τ = (m . 2l ) . B sin θ ………………..(4)
From equations (1) and (4)
τ = M B sin θ

This is an expression for the torque acting on a magnet kept in the magnetic field. The direction of the torque is perpendicular to the plane passing through .i.e. perpendicular to the plane of the paper.
Tangent Law:
Statement:
If a bar magnet is free to rotate about an axis at right angles to two mutually perpendicular uniform magnetic fields of inductions B1 and B2, then it comes to rest in a direction making an angle q with the direction of , such that
B2 = B1 . tan θ
Proof:
It is found that when a bar magnet is suspended in two cross magnetic fields, it comes to rest with its axis along the direction of the resultant of the two magnetic fields. Consider a bar magnet suspended in two cross magnetic fields B1 and B2 .

Under the action of these two magnetic fields the needle rotates through angle θ and come to rest along the resultant of these two magnetic fields.
In the equilibrium condition, the needle is acted upon by two torques. one due to the magnetic field of induction given by m B2 .2l. cosθ and second due to the horizontal component of the earth given by m B1 .2l. sin θ. Under the action of these two torques, the needle remains in equilibrium. Hence the two couples should be equal.
∴ m B2 . 2l . cos θ = m B1 . 2l. sin θ
∴ B2 . cos θ = B1 . sin θ
B2 = B1 . (sin θ / cos θ)
B2 = B1 . tan θ
This relation is called as the tangent law.
Numerical Problems on Torque Acting on Magnet:
Example – 03:
A torque of moment 25 x 10-2 Nm acts on a magnet suspended in a uniform magnetic field of induction 0.5 Wb/m2 when making an angle of 30° with the field. Find the magnetic dipole moment of the magnet.
Given: Torque = τ = 25 x 10-2 Nm, Magnetic induction = B = 0.5 Wb/m2, angle with field = θ = 30°.
To find: Magnetic moment = M = ?
Solution:
τ = MB sin θ
∴ M = τ/ Bsin θ
∴ M = 25 x 10-2/ (0.5 x sin 30°) = 25 x 10-2/ (0.5 x 0.5)
∴ M = 25 x 10-2/ (0.25) = 1 Am2
Ans: The magnetic dipole moment of the magnet is 1 Am2
Example – 04:
A magnet of magnetic dipole moment 2 Am2 is deflected through 30° from the direction of a magnetic field of induction 2 Wb/m2. Find the magnitude of the torque or couple.
Given: Magnetic moment = M = 2 Am2, Magnetic induction = B = 2 Wb/m2, angle with field = θ = 30°.
To find: Torque = τ =?
Solution:
τ = MB sin θ
∴ τ = 2 x 2 x sin 30° = 2 x 2 x 0.5 = 2 Nm
Ans: The torque acting on the magnet is 2 Nm
Example – 05:
A bar magnet of dipole moment 7.5 Am2 experiences a torque of 1.5 x 10-4 Nm, when placed inclined at 30° in a uniform magnetic field. Find the magnetic induction of the field.
Given: Magnetic moment = M = 7.5 Am2, , angle with field = θ = 30°, Torque = τ = 1.5 x 10-4 Nm
To find: Magnetic induction = B =?
Solution:
τ = MB sin θ
∴ B = τ/ Msin θ
∴ B = 1.5 x 10-4/ (7.5 x sin 30°) = 1.5 x 10-4/ (7.5 x 0.5)
∴ B = 4 x 10-5 Wb/m2
Ans: The magnetic induction is is 4 x 10-5 Wb/m2 or 4 x 10-5 T
Example – 06:
A magnet of dipole moment 0.05 Am2 is suspended so to move freely in a horizontal plane. Find the couple required to hold it at right angles to the Earth’s horizontal magnetic induction of 0.32 x 10-4 Wb/m2.
Given: Magnetic moment = M = 0.05 Am2, Magnetic induction = B = 0.32 x 10-4 Wb/m2, angle with field = θ = 90°.
To find: Torque = τ =?
Solution:
τ = MB sin θ
∴ τ = 0.05 x 0.32 x 10-4 x sin 90°
∴ τ = 0.05 x 0.32 x 10-4 x 1 = 1.6 x 10-6 Nm
Ans: The torque acting on magnet is 1.6 x 10-6 Nm
Example – 07:
Calculate the dipole moment of magnet which when placed at right angles to the earth’s horizontal magnetic induction 2 x 10-5 Wb/m2 experiences a couple of 2 x 10-5 Nm.
Given: Torque = τ = 2 x 10-5 Nm, Magnetic induction = B = 2 x 10-5 Wb/m2, angle with field = θ = 90°.
To find: Magnetic moment = M = ?
Solution:
τ = MB sin θ
∴ M = τ/ Bsin θ
∴ M = 2 x 10-5/ (2 x 10-5 x sin 90°) = 2 x 10-5/ (2 x 10-5 x 1)
∴ M = 1 Am2
Ans: The magnetic moment of the magnet is 1 Am2
Example – 08:
A magnet of moment 0.6 Am2 makes an angle of 30° with the magnetic meridian. Calculate the torque that tends to bring the magnet back to the meridian given that the earth’s horizontal field is 3.2 x 10-5 Wb/m2.
Given: Magnetic moment = M = 0.6 Am2, Magnetic induction = B = 3.2 x 10-5 Wb/m2, angle with field = θ = 90°.
To find: Torque = τ =?
Solution:
τ = MB sin θ
∴ τ = 0.6 x 3.2 x 10-5 x sin 30°
∴ τ = 0.6 x 3.2 x 10-5 x 0.5 = 9.6 x 10-6 Nm
Ans: The torque required is 9.6 x 10-6 Nm
Example – 09:
A torque of 5 x 10-3 Nm is required to hold a freely suspended horizontal bar magnet with the axis at an angle of 60° to uniform horizontal field of induction 3 x 10-3 Wb/m2. Find the magnetic moment of the magnet.
Given: Torque = τ = 5 x 10-3 Nm, Magnetic induction = B = 3 x 10-3 Wb/m2, angle with field = θ = 60°.
To find: Magnetic moment = M = ?
Solution:
τ = MB sin θ
∴ M = τ/ Bsin θ
∴ M = 5 x 10-3/ (3 x 10-3 x sin 60°)
∴ M = 5 x 10-3/ (3 x 10-3 x 0.8660)
∴ M = 1.925 Am2
Ans: The magnetic moment of the magnet is 1.925 Am2
Example – 10:
A short bar magnet placed with its axis at 30° to a uniform magnetic field of 0.2 T experiences a torque of 0.06 Nm. Calculate the magnetic moment of the magnet and find out what orientation of the magnet corresponds to stable equilibrium in magnetic field.
Given: Torque = τ = 0.06Nm, Magnetic induction =0.2 T, angle with field = θ = 30°.
To find: Magnetic moment = M = ? θ = ? for stable equilibrium.
Solution:
τ = MB sin θ
∴ M = τ/ Bsin θ
∴ M = 0.06/ (0.2 x sin 30°) = 0.06/ (0.2 x 0.5)
∴ M = 0.6 Am2
For stable equilibrium torque acting on magnet is zero.
τ = MB sin θ
∴ 0 = MB sin θ
∴ sin θ = 0
∴ θ = 0°
Ans: The magnetic moment of the magnet is 0.6 Am2 and for stable equilibrium θ = 0°
i.e. the axis of magnet should be parallel to the magnetic field.
Example – 11:
A bar magnet of moment 0.9 JT-1 experiences a torque of 0.063 Nm, when placed inclined at 30° in a uniform magnetic field. Find the magnetic induction of the field.
Given: Magnetic moment = M = 0.9 JT-1, angle with field = θ = 30°, Torque = τ = 0.063 Nm
To find: Magnetic induction = B =?
Solution:
τ = MB sin θ
∴ B = τ/ Msin θ
∴ B = 0.063/ (0.9 x sin 30°) = 0.063/ (0.9 x 0.5)
∴ B = 0.14 T
Ans: The magnetic induction is is 0.14 T.
Example – 12:
A magnet of dipole moment 6.4 Am2 and length 5 x 10-3 m makes an angle of 60° with the magnetic field of 0.4 T. calculate the torque acting on it. Also find the pole strength of the magnet.
Given: Magnetic moment = M = 6.4 Am2, Magnetic induction = B = 0.4 T, angle with field = θ = 60°, magnetic length = 5 x 10-3 m
To find: Torque = τ =? pole strength = m = ?
Solution:
τ = MB sin θ
∴ τ = 6.4 x 0.4x sin 60° = 6.4 x 0.4x 0.8860 = 2.2 Nm
M = m x magnetic length
∴ m = M/magnetic length = 6.4/5 x 10-3 = 1.28 x 103 Am
Ans: The torque required is 1.28 x 103 Nm
Example – 13:
Two magnets of magnetic moments M and √3M are joined together to form a cross. The combination is suspended freely in a uniform magnetic field. In the equilibrium position the magnet of magnetic moment M makes an angle θ with the field. Determine θ.
Solution:
The magnet of magnetic moment M makes an angle θ with the field.
As the two magnets are forming cross, the magnet of magnetic moment √3M makes an angle (90° – θ) with the field.
Let B be the magnetic strength of the external field.
For equilibrium the torque acting on the two magnets must be equal.
τ1 = τ2
∴ MB sin θ = √3MB sin (90° – θ)
∴ sin θ = √3 cos θ
∴ tan θ = √3
∴ θ = 60°
Ans: Hence the value of θ is 60°