The Energy of Particle Performing S.H.M.

Science > Physics > Oscillations: Simple Harmonic Motion > The Energy of Particle Performing S.H.M.

In this article, we shall study the concept and expression of the total energy of a particle performing S.H.M. and its constituents.

Kintetic Energy of Particle Performing Linear S.H.M.:

Consider a particle of mass ‘m’ which is performing linear S.H.M. of amplitude ‘a’ along straight line AB, with the centre O.  Let the position of the particle at some instant be at C, at a distance x from O.

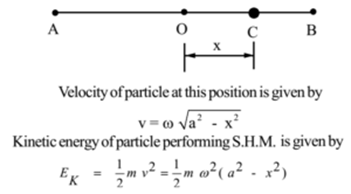
This is an expression for the kinetic energy of particle S.H.M.

Thus the kinetic energy of the particle performing linear S.H.M. and at a distance of x₁ from the mean position is given by

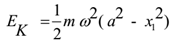
Special cases:

Case 1: Mean Position:

The kinetic energy of particle performing S.H.M. is given by

For mean position x₁ = 0

Case 2: Extreme position:

The kinetic energy of particle performing S.H.M. is given by

For mean position x₁ = a

Potential Energy of Particle Performing Linear S.H.M.:

Consider a particle of mass ‘m’ which is performing linear S.H.M. of amplitude ‘a’ along straight line AB, with the centre O.  Let the position of the particle at some instant be at C, at a distance x from O.

Particle at C is acted upon by restoring force which is given by F = – mω²x

The negative sign indicates that force is restoring force.

Let. External force F’ which is equal in magnitude and opposite to restoring force acts on the particle due to which the particle moves away from the mean position by small distance ‘dx’ as shown. Then

F’ = mω²x

Then the work done by force F’ is given by

dW =  F’ . dx

dW = mω²x dx

The work done in moving the particle from position ‘O’ to ‘C’ can be calculated by integrating the above equation

This work will be stored in the particle as potential energy

This is an expression for the potential energy of particle performing S.H.M.

Special cases:

Case 1: Mean Position:

The potential energy of particle performing S.H.M. is given by

For mean position x₁ = 0

∴ E_P = 0

Case 2: Extreme position:

The potential energy of particle performing S.H.M. is given by

For mean position x₁ = a

Total Energy of Particle Performing Linear S.H.M.:

The Kinetic energy of particle performing S.H.M. at a displacement of x₁ from the mean position is given by

The potential energy of particle performing S.H.M. at a displacement of x₁ from mean position is given by

The total energy of particle performing S.H.M. at a displacement of x₁ from the mean position is given by

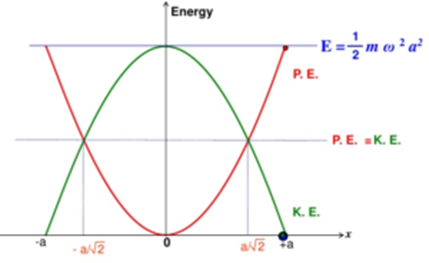
Since for a given S.H.M., the mass of body m, angular speed ω and amplitude a are constant, Hence the total energy of a particle performing S.H.M. at C is constant i.e. the total energy of a linear harmonic oscillator is conserved. It is the same at all positions. The total energy of a linear harmonic oscillator is directly proportional to the square of its amplitude.

Variation of Kinetic Energy and Potential Energy in S.H.M Graphically:

Relation Between the Total Energy of particle and Frequency of S.H.M.: 

The quantities in the bracket are constant. Therefore, the total energy of a linear harmonic oscillator is directly proportional to the square of its frequency.

Relation Between the Total Energy and Period of S.H.M.: 

The quantities in the bracket are constant. Therefore, the total energy of a linear harmonic oscillator is inversely proportional to the square of its period.

Expressions for Potential Energy, Kinetic Energy and Total Energy of a Particle Performing S.H.M. in Terms of Force Constant:

Potential energy: 

The potential energy of particle performing S.H.M. is given by

This is an expression for the potential energy of particle performing S.H.M. in terms of force constant.

Kinetic energy: 

The kinetic energy of particle performing S.H.M. is given by

This is an expression for Kinetic energy of particle performing S.H.M. in terms of force constant.

Total energy: 

The total energy of particle performing S.H.M. is given by

This is an expression for the total energy of particle performing S.H.M. in terms of force constant.

Previous Topic: Graphical Representation of S.H.M.

Next Topic: Numerical Problems on Energy of Particle

Science > Physics > Oscillations: Simple Harmonic Motion > The Energy of Particle Performing S.H.M.