Scalar Product And Vector Product

Science > Physics > Scalars and Vectors > Scalar Product And Vector Product

In this article, we shall study two types of products of vectors: a) Scalar product and b) Vector product

Scalar Product of Two Vectors:

The scalar or dot product of two vectors is defined as the product of magnitudes of the two vectors and the cosine of the angles between them.

If  a and  b are two vectors and θ is the angle between the two vectors then by the definition scalar product of two vectors

a · b = a b cos θ

Where  a = magnitude of a and b = magnitude of vector  b

Characteristics of the Scalar Product:

• The scalar product of two vectors is always a pure number i.e. the scalar product is always a scalar.
• The scalar product of two vectors is commutative. i.e. a · b =  b · a

a · b = a b cos θ = b a cos θ = b · a

• Scalar product obeys the distributive law of multiplication. i.e.  a ·( b +  c) = a · b  +  a · c
•  a and b  are two vectors perpendicular to each other, if and only if   a · b =  b · a  = 0
•  a and b  are two vectors parallel to each other, if and only if   a · b =  b · a  = ab
• If  a =  a_x i + a_y j + a_z k and b = b_x i + b_y j + b_z k are the two vectors, then their scalar product is given by

  a · b =(a_x b_x + a_y b_y + a_z b_z )

• The scalar product of two vectors may be zero or positive or negative.

Scalar Products of Standard Unit Vectors:

i · i = i × i cos 0° = 1 × 1× 1 = 1, Similarly,  We have j · j = 1  and  k · k = 1

i · j = i · j = i × j cos 90° = 1 × 1× 0 = 0, Similarly, We have j · k = k · j = o and k · i = i · k = 0

Expression for Scalar Product of Two Vectors:

If  a =  a_x i + a_y j + a_z k and b = b_x i + b_y j + b_z k are the two vectors, then the scalar product is given by

a · b  = ( a_x i + a_y j + a_z k ) · (b_x i + b_y j + b_z k )

∴ a · b  =  a_x i · (b_x i + b_y j + b_z k ) + a_y j · (b_x i + b_y j + b_z k )  + a_z k · (b_x i + b_y j + b_z k )

∴ a · b  =  a_xb_x  i ·i + a_xb_y  i ·j +  a_xb_z   i ·k  +  a_y b_x  j ·i+ a_y b_y j ·j + a_y b_z j ·k

+ a_zb_x  k ·i + a_zb_y k ·j   +  a_zb_z k ·k

∴ a · b  =  a_xb_x (1) + a_xb_y (0) +  a_xb_z (0) +  a_y b_x(0) +  a_y b_y (1) + a_y b_z (0)

+ a_zb_x  (0) + a_zb_y (0)  +  a_zb_z (1)

∴ a · b  =  a_xb_x  +  a_y b_y   +  a_zb_z 

This is an expression for scalar product of two vectors.

Examples of Scalar Product of Two Vectors:

• Work done is defined as scalar product as W = F · s, Where F is a force and s  is a displacement produced by the force
• Power is defined as a scalar product as P = F · v, Where F  is a force and v  is a velocity.

Notes:

• if two vectors are perpendicular to each other then θ = 90° , thus cos θ  = cos 90° = 0 Hence  a · b  =  ab cos 90° = ab(0) = 0
• if two vectors are parallel  to each other then θ = 0° , thus cos θ  = cos 0° = 1 Hence a · b = ab cos 0° = ab(1) = ab
• if two vectors are equal  to each other then θ = 0° , thus cos θ  = cos 0° = 1 Hence  a · a  =  aa cos 0° = aa(1) = a²

Vector Product of Two Vectors:

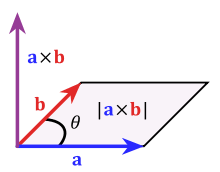
The vector or cross product of two vectors is a vector whose magnitude is equal to the product of the magnitudes of the two vectors and the sine of the angle between the two vectors.

If a and  b are two vectors and θ is the angle between the two vectors then by the definition  of the vector  product of two vectors

a × b = a b sin θ n

Where  a = magnitude of a and b = magnitude of vector  b

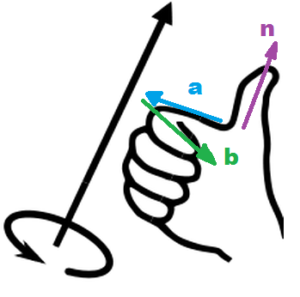
n = unit vector perpendicular to the plane of a and  b

The direction of n is given by right-hand thumb rule

Characteristics of the Vector product:

• Vector product two vectors is always a  vector.
• The Vector product of two vectors is noncommutative. i.e.  a · b ≠  b · a but a · b = –  b · a
• vector product obeys the distributive law of multiplication. i.e.  a ×( b +  c) = a  ×  b  +  a ×  c
• If a · b = 0 and a ≠ o, b ≠ o then the two vectors are parallel to each other.
• If  a =  a_x i + a_y j + a_z k and b = b_x i + b_y j + b_z k are the two vectors, then their vector product is given by

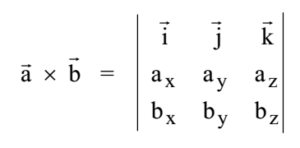
Direction of Vector Product By Right Hand Thumb or Grip Rule:

Hold the right hand along the first vector such that the fingers are parallel to the plane of the vectors and the curled fingers are along the angular direction in which we have to move to the second vector then the outstretched thumb indicates the direction of the vector obtained by vector product of two vectors.

Vector Products of Standard Unit Vectors:

i × i = i × i sin 0° = 1 × 1× 0 = 1, Similarly,  We have j × j = 0  and  k × k = 0

Using the reference circle for vector product

i × j = k ,  j × i = – k  ; j × k = i ,  k × j = – i  ;  k × i = j ,  i × k = – j  ;

Expression for the Vector Product of Two Vectors:

If  a =  a_x i + a_y j + a_z k and b = b_x i + b_y j + b_z k are the two vectors, then the scalar product is given by

a × b  = ( a_x i + a_y j + a_z k ) × (b_x i + b_y j + b_z k )

∴ a × b  =  a_x i × (b_x i + b_y j + b_z k ) + a_y j × (b_x i + b_y j + b_z k )  + a_z k × (b_x i + b_y j + b_z k )

∴ a × b  =  a_xb_x  i × i + a_xb_y  i × j +  a_xb_z   i × k  +  a_y b_x  j × i+ a_y b_y j × j + a_y b_z j × k

+ a_zb_x  k × i + a_zb_y k × j   +  a_zb_z k × k

∴ a × b  =  a_xb_x (0) + a_xb_y (k) +  a_xb_z (- j ) +  a_y b_x(- k) +  a_y b_y (0) + a_y b_z (i)

+ a_zb_x  (j) + a_zb_y (- i)  +  a_zb_z (0)

∴ a × b  =  a_xb_y k  –  a_xb_z j –  a_y b_xk +  a_y b_z i + a_zb_x  j – a_zb_y i

∴ a × b  =  a_y b_z i  – a_zb_y i  –  a_xb_z j + a_zb_x  j    +  a_xb_y k   –  a_y b_xk

∴ a × b  =  i( a_y b_z – a_zb_y) –   j(a_xb_z + a_zb_x)    +  k(a_xb_y    –  a_y b_x )

This is an expression for vector product of two vectors.

Examples of Vector Product of Two Vectors:

• Torque acting on the rotating body is defined as vector product τ = r × F, Where F is a force and r  is a position vector of the point of action of the force.
• If a and b are the adjacent sides of a parallelogram, then the area of the parallelogram is given as A =  | a × b|
• If a and b are the adjacent sides of a triangle, then the area of the triangle is given as A =  ½| a × b|

Previous Topic: Vector Algebra

For More Topics in Physics Click Here

Science > Physics > Scalars and Vectors > Scalar Product And Vector Product