Viscosity

Some liquids like water Kerosene flow very easily while some liquids like honey, glycerine do not flow easily. The property by virtue of which a liquid or a fluid opposes the relative motion between two adjacent layers is called viscosity. The force which opposes the relative motion between two adjacent layers in a fluid is called viscous force for viscous drag or internal friction. The force of viscosity in the case of liquids is analogous to the friction force in the case of solids.

Viscosity describes the internal friction of a moving fluid. A fluid with large viscosity resists motion because its molecular makeup gives it a lot of internal friction. A fluid with low viscosity flows easily because its molecular makeup results in very little friction when it is in motion. Gases also have viscosity, although it is a little harder to notice it in ordinary circumstances. There are two kinds of viscosity commonly reported, kinematic and dynamic. Dynamic viscosity is the relationship between the shear stress and the shear rate in a fluid. The Kinematic viscosity is the relationship between viscous and inertial forces in a fluid.

Practical Examples of Viscosity:

• The body of fishes, the hull of ships, torpedoes, and submarines is such that the opposition to their motion in the liquid (water) is minimum. The shapes of bullets, arrows, racing cars, jet planes, bombs are such that opposition to their motion in air i.e. viscous resistance is minimum. This design work is called streamlining of the shapes and shapes themselves are called streamlined shapes.
• The quality of fountain ink depends on the viscosity of the ink.
• Blood circulation in our body depends on the viscosity of blood.
• Lubricating oils used in heavy machines is more viscous than those used in light machines. Thus car engine requires lubricating oil with a higher viscosity than lubricating oil required for the watch.

Effect of Change of Temperature and Pressure on Viscosity:

Temperature and pressure affect the viscosity of a fluid. The viscosity of liquids increase rapidly with an increase in temperature. On increasing pressure viscosity of liquid molecules increases due to the increase in the resistance to the flow of liquid.

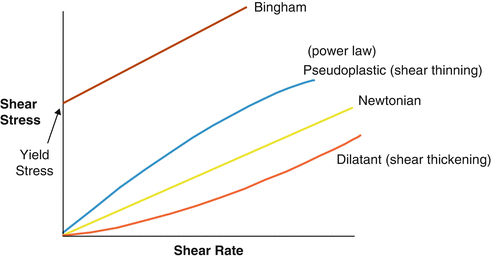
If the viscosity does not change with pressure, we describe something as being a Newtonian fluid. And, if the viscosity does change as stress or temperature changes, we describe something as being a non-Newtonian fluid. Water is an example of Newtonian fluid and toothpaste is an example of Non-Newtonian fluid.

Newtonian fluids obey Newton’s law of viscosity. The viscosity is independent of the shear rate. Examples: water, mineral oil, gasoline, alcohol

Non-Newtonian fluids do not follow Newton’s law and, thus, their viscosity (ratio of shear stress to shear rate) is not constant and is dependent on the shear rate. Example: tooth paste

When shear is applied, the viscosity of non-Newtonian fluids decreases or increases, depending on the fluid. The behaviour of the fluid can be described in one of four ways:

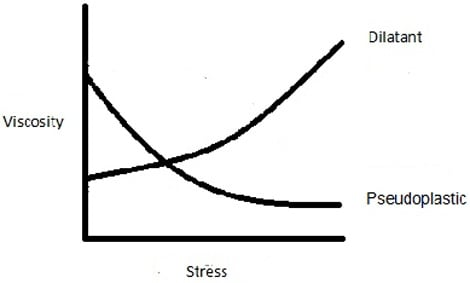
Dilatant: In this case, the viscosity of the fluid increases when shear is applied. Examples: quicksand, cornflour and water, silly putty.

Pseudoplastic: Pseudoplastic is the opposite of dilatant; the more shear applied, the less viscous it becomes. For example: Ketchup

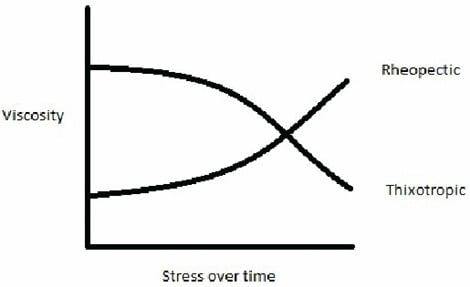
Rheopectic: Rheopectic is very similar to dilatant in that when shear is applied, viscosity increases. The only difference here is that viscosity increase is time-dependent. Examples: gypsum paste, cream

Thixotropic: Fluids with thixotropic properties decrease in viscosity when shear is applied. This is a time-dependent property as well. Examples: paint, cosmetics, asphalt, glue.

It’s important to fully understand the properties of the fluids you’re transferring, mixing, or pumping because viscosity plays a major role in sizing and selecting equipment. Understanding how it reacts to shear will help you properly size and select all the equipment it touches. 

Types of Flow:

Streamline Flow:

When liquid flows slowly so that its velocity is less than a certain value called the critical velocity of flow or the streamline velocity of flow, then the flow of liquid is called streamline flow. Streamline flow is also called as laminar flow. e.g. Flow of water in the canal.

Characteristics of Streamline Flow:

• For streamline flow, the velocity of the flow of liquid is less than or equal to critical velocity.
• In streamline flow, the velocity at any given point of the liquid always remains constant.
• In streamline flow liquid can be assumed to be made up of distinct layers sliding over each other such that each layer has constant velocity.
• In streamline flow molecules in each layer move forward in the same layer only.
• For streamline flow velocity gradient is constant.

Turbulent flow:

When liquid flows fast so that its velocity is greater than a certain value called the critical velocity of flow or the streamline velocity of flow, then the flow of liquid is called turbulent flow. Turbulent flow is also called as non-laminar flow. e. g. The flow of water in the river.

Characteristics of Turbulent Flow:

• For turbulent flow, the velocity of the flow of liquid is greater than the critical velocity.
• In turbulent flow, the velocity at any given point of the liquid does not remain constant.
• In turbulent flow, the liquid does not move forward in the form of layers.
• In turbulent flow molecules of liquid can move in any layer.
• For turbulent flow velocity gradient is not constant.

Origin of Viscosity:

Consider the motion of fluid over a horizontal surface such that its velocity of flow is slow then we can observe that the velocity of the layer which is contact with the surface is zero.

Velocities of other layers increase with an increase in the distance of the layer from the solid surface. If we consider a particular layer we can see that the layer immediately above it moves faster than the layer immediately below it. Thus the upper layer will try to move the lower layer with higher velocity and vice versa. In fact, the two layers together try to destroy relative motion as if some backward drag were acting tangentially between the two layers. This backward drag opposing the flow of liquid is called viscosity.

The velocity of any layer of liquid depends on its distance from the fixed layer. Let v and v + dv be the velocities of two layers situated at a distance of x and x + dx from the fixed layer. Then the ratio dv/dx is called the velocity gradient.

The velocity gradient of flow is defined as the rate of change of velocity with respect to the distance from the fixed layer.

Newton’s Law of Viscosity:

Statement:

Viscous force (F) acting on any layer of liquid is directly proportional to

• the area of the layer (A) and
• the velocity gradient (dv/dx)

Explanation:

By Newton’s law of viscosity

F ∝ A ….(1)

F ∝ dv/dx  ……..(2)

from (1) & (2)

F ∝ A . dv/dx

F =  η . A . dv/dx

This formula is known as Newton’s formula of viscosity. Where η (eta) is called the coefficient of viscosity. The value of η depends upon temperature & the nature of the liquid.

Coefficient of Viscosity:

By Newton’s formula

F =  η . A . dv/dx

let A = 1 unit and  dv/dx = 1 unit

then, F = η  i.e. η = F

The coefficient of viscosity of a liquid is defined as the tangential viscous force acting on the unit area of liquid lair per unit velocity gradient.

SI Unit of η is N.s/m². CGS unit of η is poise

1 poise = 0.1 N.s/ m² and 1 centipoise = 10^{– 2} poise

Relation between S.I. and c.g.s. units of Coefficient of Viscosity:

The S.I. unit of viscosity is Ns / m² and c.g.s unit is dyne-s / cm² i.e.  poise.

Now, 1 N  = 10 ⁵ dyne and 1m = 100 cm

1   Ns / m² = 10 ⁵ dyne × s / (100 cm)²    = 10 ⁵ dyne × s / 10⁴ cm² 

1   Ns / m² = 10  dyne × s / cm²

Dimension of Coefficient of Viscosity (η) :

By Newton’s formula,

Hence dimensions of the coefficient of viscosity are [L^-1M¹T^-1]

The SI unit of the coefficient of viscosity is Ns m^-2 or decapoise or pascal second.

Hence the coefficient of viscosity of a liquid is 1 decapoise or 1Ns m^-2, if a tangential force of 1 N is required to maintain a velocity gradient of 1 s^-1 between two parallel layers each of area 1 m².

Note:

• Viscosity of an ideal liquid is zero. Practically no such liquid exists. Every liquid has some viscosity.
• The coefficient of viscosity of a liquid is inversely proportional to its temperature.
• The coefficient of viscosity of a gas is directly proportional to its temperature.

Similarities between Fluid Friction (Viscosity) and Solid Friction:

• Both come into play whenever there is a relative motion.
• Both oppose relative motion
• Both arises from intermolecular forces
• Both depend on nature of surface
• Both acts tangentially in opposite direction to that of motion.
• Both friction and viscosity exhibit the intensive property of the matter, as they remain the same even if the amount of the matter changes.

Differences between Fluid Friction (Viscosity) and Solid Friction:

Viscosity	Friction
Viscosity is a measure of a fluid’s resistance to flow.	Friction is defined as the resistance offered by the surfaces that are in contact when they move past each other.
It is an internal force, which acts between the two layers of fluid.	It is a force that acts between the two solid surfaces.
It depends on the area of contact and the velocity gradient between the layers.	It is independent of area of contact and of the relative velocity of the two surfaces.
It depends on the temperature of the fluid. It is inversely proportional to temperature.	It is a temperature-independent quantity.
In this case heat is generated within the fluid and not at the interface of the solid and fluid.	In this case heat is generated at the surfaces between the solids.

Significance of Viscosity:

• Viscosity is a measure of whether the flow is laminar or turbulent. 
• Behaviour of viscosity helps to design a machine in mechanical engineering, to build a ship, to work in marine condition.
• If there are no viscosity fluid would have no internal resistance and so it will flow forever before facing any barrier.
• From the behaviour of viscosity with temperature, we can find whether the fluid is liquid or gas. For increasing the temperature the viscosity will increase for gas. On the other hand, increasing the temperature will decrease the Viscosity for Liquid. 
• The viscosity of blood depends on the concentration of the red blood corpuscles in it. Thus viscosity of blood can be used to detect blood corpuscles deficiency.
• In lubrication, the viscosity is the most needed characteristic of lubricating oil. Lubricating oil should have proper value of viscosity so that it can form a lubricating layer easily without shear.
• Viscosity of air or liquid is used in providing damping torque in measuring instruments.
• Viscosity is a critical property of hydraulic oil used in valves and pumps.
• For greases, the viscosity is an important element too.
• The viscosity of liquid is very important in hydraulic brakes.
• Blood circulation through arteries is dependent on the viscosity of the blood.

Measurement of Viscosity:

U-Tube Viscometer

U-tube viscometers are also known as glass capillary viscometers or Ostwald viscometers. A viscometer consists of two reservoir bulbs and a capillary tube. In one arm of the U is the capillary, a vertical section of a precise narrow bore. Above which is a bulb, with it is another bulb lower down on the other arm as shown in the figure.

In use, the upper bulb draws the liquid by suction, then the liquid is made to flow down through the capillary into the lower bulb. Two marks (one above and one below the upper bulb) indicate a known volume. The time taken for the liquid to pass between these marks is measured using stopwatch. This time is proportional to the kinematic viscosity. By multiplying the time measured by the conversion factor of the viscometer, the kinematic viscosity is obtained.

Stokes’ Law:

Statement:

The viscous drag on a spherical body moving with sufficiently small velocity through a viscous medium or the medium moves past the spherical body with streamline flow is directly proportional to

• the radius ‘r’ of the sphere,
• the relative velocity ‘v’ of the sphere through the medium. And
• the coefficient of viscosity ‘η’ of the medium.

Mathematical Expression of Stokes’ Law:

F = 6 π η r v

Derivation of  Stokes’ law Using Dimensional Analysis:

Let (F) be the viscous force acting on a spherical body such that it depends on the radius of spherical body (r) terminal velocity (v) and coefficient of viscosity (η).

F ∝ r ^x ….(1)

F ∝ v ^y ….(2)

F ∝ h ^z ….(3)

From (1), (2) & (3)

F ∝ r ^x v ^y η ^z

∴ F =    k r ^x v ^y η ^z  ……….(4)

∴  [F] =   [r]^x [v]^y [η]^z

∴  [L¹M¹T^-2] = [L¹M⁰T⁰]^x [L¹M⁰T^-1]^y [L^-1M¹T^-1]^z

∴  [L¹M¹T^-2] = [L^xM⁰T⁰] [L^yM⁰T^-y] [L^-zM^zT^-z]

∴  [L¹M¹T^-2] = [L^x+y-zM^zT^{-y -z}]

Considering equality of two sides we have

x + y – z = -1, z = 1, -y – z = -2 i.e. y + z = 2

Substituting z = 1 in equation y + z = 2, we get  y = 1

Substituting y = 1, z = 1 in  equation x + y + z = -1, we get x = 1

Substituting x = 1, y = 1, and z = 1 in  equation (4) we get

F =    k r v η

Experimentally the value of k  is found to be 6π

∴  F =    6π η r v

Thus Stoke’s law is proved.

Terminal Velocity:

When a smooth rigid body is allowed to fall through a viscous fluid it carries with it the layers of the liquid in contact. This tends to produce a relative motion between the layers of fluid which is opposed by viscous force.

The opposing force increases with the increases in the velocity of the body in case of small bodies the opposing force becomes equal to the driving force and the body start going down in fluid with constant velocity.  This constant velocity is called terminal velocity.

Expression for Terminal Velocity of a Spherical Body:

Consider a small sphere of density ρ and radius ‘r’ falls under gravity through a medium of density σ and coefficient viscosity η. As the sphere begins to fall down its velocity goes on increasing due to gravitational force acting on it. But as the velocity increases the opposing viscous force also increases. When the viscous force becomes equal and opposite to the gravitational force, the resultant force acting on the sphere becomes zero and the sphere begins to fall with the constant velocity it has already acquired. This velocity is known as terminal velocity.

Downward force =   Weight of the body = mg = V ρ g

Upward force = viscous force +  upthrust due to medium

∴ Upward force = Viscous force + weight of displaced medium

∴ Upward force = 6π η r v  + V σ g

But, Downward force = Upward force

∴ V ρ g = 6π η r v  + V σ g

∴   6π η r v = V ρ g – V σ g

∴   6π η r v = V (ρ  – σ) g

This is an expression for terminal velocity of a sphere