Science > Physics > Current Electricity > Numerical Problems on Wheatstone’s Metre Bridge 02
Example – 15:
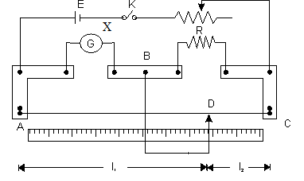
In Wheatstone’s metre bridge experiment with unknown resistance X in the left gap and 60 Ω resistance in a right gap null point is obtained at l cm from the left end. If the unknown resistance is shunted by equal resistance, what should be the value of resistance in the right gap in order to get the null point at the same point?
Solution:
Case – I:
Given: resistance in the left gap = X Ω, Resistance in right gap = 60 Ω
l is the distance of the null point from the left end.
For balanced metre bridge
∴ X/60 = l / (100 – l) …………. (1)
Case – II:
Given: X Ωresistance is shunted by X Ω, Resistance in the left gap = (X x X)/(X + X) = X²/2X = X/2 Ω,
Let the resistance in right gap be R Ω
Again l is the distance of the null point from the left end.
For balanced metre bridge

∴ (X/2)/R = l / (100 – l)
∴ X/2R = l / (100 – l) ………….. (2)
From equations (1) and (2)
∴ X/60 = X/2R
∴ 2R = 60
∴ R = 30 Ω
Ans: The resistance in the right gap should be 30 Ω
Example – 16:
With resistance R1 in the left gap and R2 in the right gap of a Wheatstone’s metre bridge, the null point is obtained at 30 cm from the right end. When R1 is reduced by 2 Ω and R2 is increased by 2 Ω, the null point is obtained at 30 cm from the left end. Find R1 and R2.
Solution:
Case – I:
Given: Resistance in left gap = R1, Resistance in right gap = R2
Null point from right end = 100 – l = 30 cm
Null point from left end = l = 100 – 30 = 70 cm
For balanced metre bridge

∴ R1/R2 = 70/30= 7/3
∴ R1 = (7/3)R2 ………. (1)
Case – II:
Given: Resistance in left gap = R1 – 2 Ω Resistance in right gap = R2 + 2 Ω
Null point from left end = l = 30 cm and 100 – l = 100 – 30 = 70 cm
For balanced metre bridge

∴ (R1 – 2)/(R2 + 2) = 30/70= 3/7
∴ 7R1 – 14 = 3R2 + 6
∴ 7R1 – 3R2 = 20
∴ 7 (7/3)R2 – 3R2 = 20
∴ (49/3)R2 – 3R2 = 20
∴ ((49 – 9)/3)R2 = 20
∴ (40/3)R2 = 20
∴ R2 = 20 x (3/40) = 1.5 Ω
R1 = (7/3)R2 = (7/3) x 1.5 = 3.5 Ω
Ans: R1 = 3.5 Ω and R2 = 1.5 Ω
Example – 17:
Two coils are connected in series in one gap of Wheatstone’s metre bridge and the null point is obtained at the midpoint of wire when a 50 Ω resistance is connected in the right gap. The two coils are then connected in parallel and it is found that the resistance in other gap is to be changed by 38 Ω to get the null point at the same point as before. Find the resistance of the coils.
Solution:
Let R1 and R2 be the resistances of the two coils
Case – I:
Given: R1 and R2 be in series, resistance in left gap = R1 + R2, Resistance in right gap = 50 Ω, l = 50 cm and, 100 – l = 100 – 50 = 50 cm
For balanced metre bridge

∴ (R1 + R2)/50 = 50/50
∴ (R1 + R2) = 50 ………. (1)
Case – II:
Now the two coils are connected in parallel. Hence their effective resistance is decreasing. To keep the null point at the same point, the resistance in the right gap should also decrease.
Hence resistance in the right gap = 50 – 38 = 12 Ω

∴ R1 (50 – R1 ) = 600
∴ 50R1 – R12 = 1350
∴ R12 – 50 R1 + 600 = 0
∴ (R1 – 30)(R1 – 20) = 0
∴ R1 = 30 Ω or R11 = 20 Ω
Hence R2 = 20 Ω or R2 = 30 Ω
Ans: The restances of two coils are 30 Ω and 20 Ω.
Example – 18:
Two diametrically opposite points of a metal ring are connected by two wires in the left gap of a Wheatstone’s metre bridge. A resistance of 11 Ω. is connected in a right gap and the null point is obtained at a distance of 45 cm from the left end. Find the resistance of the metal ring.
Solution:

Let 2R be the resistances of the metal ring. As the diametrically opposite points are connected in the left gap. The resistance of each half is R and these two halves are connected in parallel.
Thus resistance in left gap = (R x R)/(R + R) = R²/2R = R/2 Ω, Resistance in right gap = 11 Ω
l = 45 cm and, 100 – l = 100 – 45 = 55 cm
For balanced metre bridge

∴ (R/2)/11 = 45/55
∴ (R/2) = 45/5 = 9
∴ R = 18 Ω
Now resistance of ring = 2R = 2 x 18 = 36 Ω
Ans: The resitance of the ring is 36 Ω.
Example – 19:
Two diametrically opposite points of a metal ring are connected by two wires in the left gap of a Wheatstone’s metre bridge. A resistance of 15 Ω. is connected in a right gap and the null point is obtained at a distance of 40 cm from the left end. Find the resistance of the wire bent in the shape of a ring.
Solution:

Let 2R be the resistances of the metal ring. As the diametrically opposite points are connected in left gap. The resistance of each half is R and these two halves are connected in parallel.
Thus resistance in left gap = (R x R)/(R + R) = R²/2R = R/2 Ω,
Resistance in right gap = 15 Ω
l = 40 cm and, 100 – l = 100 – 40 = 60 cm
For balanced metre bridge

∴ (R/2)/15 = 40/60
∴ (R/2) = 40/4 = 10
∴ R = 20 Ω
Now resistance of ring = 2R = 2 x 20 = 40 Ω
Ans: The resitance of the ring is 40 Ω.
Example – 20:
Two diametrically opposite points of a metal ring are connected by two wires in the left gap of a Wheatstone’s metre bridge. A resistance of 25 Ω. is connected in a right gap and the null point is obtained at a distance of 33.3 cm from the left end. Find the resistance of the metal ring.
Solution:

Let 2R be the resistances of the metal ring. As the diametrically opposite points are connected in left gap. The resistance of each half is R and these two halves are connected in parallel.
Thus resistance in left gap = (R x R)/(R + R) = R²/2R = R/2 Ω,
Resistance in right gap = 25 Ω
l = 33.3 cm and, 100 – l = 100 – 33.3 = 66.7 cm
For balanced metre bridge

∴ (R/2)/25 = 33.3/66.7
∴ R = (33.3/66.7) x 25 x 2
∴ R = 24.96 Ω
Now resistance of ring = 2R = 2 x 24.96 = 49.92 Ω
Ans: The resitance of the ring is 49.92 Ω.
Example – 21:
Two resistance wires of the same material have diameters in the ratio 2:1 and the lengths in the ratio 4:1 are connected in left and the right gaps of Wheatstone’s metre bridge. Find the position of the null point from the left end.
Solution:
Let R1 and R2 be the resistances of the two wires connected in left and right gaps. The material of wires is the same, hence resistivity is the same ρ1 = ρ2

Thus resistance in the left gap = R1 Ω, Resistance in right gap = R2 Ω
Let l be the position of the null point from the left end
For balanced metre bridge

∴ R1/R2 = l / (100 – l)
∴ 1 = l / (100 – l)
∴ 100 – l = l
∴ 2l = 100
∴ l = 50 cm
Ans: The position of the null point from the left end is 50 cm
Example – 22:
Equal lengths of wires of material A and B are connected in the left gap and the right gap of a Wheatstone’s metre bridge to get a null point at 30 cm from the left end. Find the ratio of diameters of wires A and B. Specific resistance of A is 5 x 10-8 Ωm and of B is 2 x 10-6 Ωm.
Solution:
Let RA and RB be the resistances of the two wires connected in left and right gaps.
Resistance in left gap = RA Resistance in right gap = RB
Null point from left end = l = 30 cm and 100 – l = 100 – 30 = 70 cm
For balanced metre bridge

∴ RA/RB = 30/70= 3/7 …………. (1)
ρA = 5 x 10-8 Ωm, ρB = 2 x 10-6 Ωm
Let rA and rB be the radii of the two wires

Ans: The ratio of diameters of two wires is 0.242:1
Example – 23:
Equal lengths of wires of manganin(ρ1) and nichrome (ρ2) are connected in the left gap and the right gap of Wheatstone’s a metre bridge to get a null point at 40 cm from the left end. Find the ratio of diameters of wires A and B. Specific resistance of manganin is 4.8 x 10-8 Ωm and of nichrome is 10-6 Ωm.
Solution:
Let R1 and R2 be the resistances of the two wires connected in left and right gaps.
Resistance in left gap = R1 Resistance in right gap = R2
Null point from left end = l = 40 cm and 100 – l = 100 – 40 = 60 cm
For balanced metre bridge

∴ R1/R2 = 40/60= 2/3 …………. (1)
ρ1 = 4.8 x 10-8 Ωm, ρ2 = 10-6 Ωm
Let r1 and r2 be the radii of the two wires

Ans: The ratio of diameters of two wires is 0.2683:1
Example – 24:
A uniform wire is cut into two pieces are so that their lengths are in the ratio 1:2. When these pieces are connected in parallel in the left gap of the Wheatstone’s metre bridge, with a resistance 25 Ω in a right gap, the null point is obtained at a distance of 40 cm from the left end of the wire. Find the resistance of the wire before it was cut into two pieces.
Solution:
Let R be the resistance of the uncut wire. Let R1 and R2 be the resistances of the two cut wires
R = R1 + R2
Ratio of their lengths l1/l2 = 1/2
The material of wires is the same, hence resistivity is the same ρ1 = ρ2
The wire is uniform, hence radii are the same r1 = r2


Resistance in left gap = (2/3)R1, Resistance in right gap = 25
Null point from left end = l = 40 cm and 100 – l = 100 – 40 = 60 cm
For balanced Wheatstone’s metre bridge

∴ (2/3)R1/25 = 40/60= 2/3
∴ R1/25 = 1
∴ R1 = 25 Ω
R2 = 2R1 = 2 x 25 = 50 Ω
Resistance of uncut wire = R = R1 + R2 = 25 + 50 = 75 Ω
Ans: The resistance of the wire before it was cut into two pieces is 75 Ω.
Example – 25:
A uniform wire is cut into two pieces are so that one piece is twice as long as the other. When these pieces are connected in parallel in the left gap of the Wheatstone’s metre bridge, with a resistance 20 Ω in a right gap, the null point is obtained at a distance of 60 cm from the right end of the wire. Find the resistance of the wire before it was cut into two pieces.
Solution:
Let R be the resistance of the uncut wire. Let R1 and R2 be the resistances of the two cut wires
R = R1 + R2
Ratio of their lengths l1/l2 = 1/2
The material of wires is the same, hence resistivity is the same ρ1 = ρ2
The wire is uniform, hence radii are the same r1 = r2


Resistance in left gap = (2/3)R1, Resistance in right gap = 25
Null point from left end = l = 100 – 60 cm = 40 cm and 100 – l = 100 – 40 = 60 cm
For balanced Wheatstone’s metre bridge

∴ (2/3)R1/20 = 40/60= 2/3
∴ R1/20 = 1
∴ R1 = 20 Ω
R2 = 2R1 = 2 x 20 = 40 Ω
Resistance of uncut wire = R = R1 + R2 = 20 + 40 = 60 Ω
Ans: The resistance of the wire before it was cut into two pieces is 60 Ω.
Previous Topic: More Problems on Metre Bridge
One reply on “Numerical Problems on Wheatstone’s Metre Bridge 02”
Super questions I really enjoyed