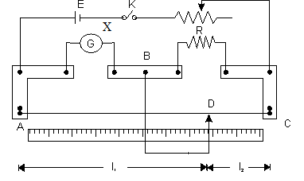
Science > Physics > Current Electricity > Numerical Problems on Wheatstone’s Metre Bridge 01
In this article and the next article, we shall study numerical problems based on Wheatstone’s metre bridge.
Example – 01:
A resistance of 10 Ω is connected in a left gap of a metre bridge. Two resistors of 20 Ω and 16 Ω are connected in parallel in the right gap. Find the position of a null point on the bridge wire.
Given: resistance in left gap = X = 10 Ω, in right gap 20 Ω and 16 Ω are in parallel, Resistance in right gap R = (20 x 16)/(20 + 16) = 320/36 = 80/9 Ω
To Find: Position of null point = l = ?
Solution:
Let l be the distance of the null point from the left end.
For balanced metre bridge

∴ 10/(80/9) = l / (100 – l)
∴ 9/8 = l / (100 – l)
∴ 9(100 – l )= 8 l
∴ 900 – 9l = 8 l
∴ 17 l = 900
∴ l = 900/17 = 52.94 cm
Ans: The null point is at 52.94 cm on the wire from the left end.
Example – 02:
A metre bridge is balanced with a 20 Ω resistance in the left gap and a 40 Ω resistance in the right gap. If 40 Ω resistance is now shunted with another of like resistance, find the shift in the null point.
Solution:
Case – I:
Given: resistance in the left gap = 20 Ω, Resistance in the right gap = 40 Ω
Let l cm be the distance of the null point from the left end.
For balanced metre bridge

∴ 20/40 = l / (100 – l)
∴ 1/2 = l / (100 – l)
∴ 100 – l = 2 l
∴ 3 l = 100
∴ l = 100/3 cm from left end
Case – II:
Given: 40 Ω resistance is shunted by 40 Ω, resistance in left gap = 20 Ω, Resistance in right gap = (40 x 40)/(40 + 40) = 1600/80 = 20 Ω
Let l cm be the distance of the null point from the left end.
For balanced metre bridge

∴ 20/20 = l / (100 – l)
∴ 1= l / (100 – l)
∴ 100 – l = l
∴ 2 l = 100
∴ l = 50 cm from left end
Shift in null point = 50 – 100/3 = 50/3 = 16.67 cm towards right
Ans: Shift in null point is 16.67 cm towards the right
Example – 03:
A metre bridge is balanced with a 20 Ω resistance in the left gap and a 30 Ω resistance in the right gap. If 20 Ω resistance is now shunted with another 20 Ω resistance, find the shift in the null point.
Solution:
Case – I:
Given: resistance in the left gap = 20 Ω, Resistance in the right gap = 30 Ω
Let l cm be the distance of the null point from the left end.
For balanced metre bridge

∴ 20/30 = l / (100 – l)
∴ 2/3 = l / (100 – l)
∴ 200 – 2l = 3 l
∴ 5 l = 200
∴ l = 40 cm from left end
Case – II:
Given: 20 Ωresistance is shunted by 20 Ω, Resistance in left gap = (20 x 20)/(20 + 20) = 400/40 = 10 Ω, resistance in left gap = 30 Ω,
Let l cm be the distance of the null point from the left end.
For balanced metre bridge

∴ 10/30 = l / (100 – l)
∴ 1/3= l / (100 – l)
∴ 100 – l = 3l
∴ 4 l = 100
∴ l = 25 cm from left end
Shift in null point = 40 – 25 = 15 cm towards left
Ans: Shift in null point is 15 cm towards the left.
Example – 04:
When two resistance coils are connected in series in one gap of metre bridge with a resistance of 75 Ω in the right gap, the null point is obtained at the midpoint of the bridge wire. The coils are then connected parallel and inserted in one gap with resistance 18 Ω in the other gap to obtain the null point at the same point as before. Find the resistance of each coil.
Solution:
Let R1 and R2 be the resistances of the two coils
Case – I:
Given: R1 and R2 be resistance in left gap = R1 + R2, Resistance in right gap = 75 Ω, l = 50 cm and, 100 – l = 100 – 50 = 50 cm
For balanced metre bridge

∴ (R1 + R2)/75 = 50/50
∴ (R1 + R2) = 75 ………. (1)
Case – II:
Given: R1 and R2 parallel in left gap, Resistance in right gap = 18 Ω

∴ R1 (75 – R1 ) = 1350
∴ 75R1 – R12 = 1350
∴ R12 -75 R1 + 1350 = 0
∴ (R1 – 30)(R1 – 45) = 0
∴ R1 = 30 Ω or R11 = 45 Ω
Hence R2 = 45 Ω or R2 = 30 Ω
Ans: The restances of two coils are 30 Ω and 45 Ω.
Example – 05:
When two resistance coils are connected in series in one gap of metre bridge with a resistance of 75 Ω in the right gap, the null point is obtained at the midpoint of the bridge wire. The coils are then connected parallel and inserted in one gap with resistance in the other gap changed by 57 Ω to obtain the null point at the same point as before. Find the resistance of each coil.
Solution:
Let R1 and R2 be the resistances of the two coils
Case – I:
Given: R1 and R2 be resistance in left gap = R1 + R2, Resistance in right gap = 75 Ω, l = 50 cm and, 100 – l = 100 – 50 = 50 cm
For balanced metre bridge

∴ (R1 + R2)/75 = 50/50
∴ (R1 + R2) = 75 ………. (1)
Case – II:
When the coils are connected in parallel, their effective resistance decreases. Hence the resistance in the left gap decreases but the null point is remaining the same. It means resistance in the right gap also decreases.
Resistance in the right gap = 75 – 57 = 18 Ω

∴ R1 (75 – R1) = 1350
∴ 75R1 – R12 = 1350
∴ R12 -75 R1 + 1350 = 0
∴ (R1 – 30)(R1 – 45) = 0
∴ R1 = 30 Ω or R11 = 45 Ω
Hence R2 = 45 Ω or R2 = 30 Ω
Ans: The resistances of two coils are 30 Ω and 45 Ω
Example – 06:
With resistances X and Y ohm in left and right gaps respectively of a metre bridge, the point is obtained at 30 cm from the left of the wire. When Y is shunted with 15 Ω resistance, the shift in null point is 10 cm.
Solution:
Case – I:
Given: resistance in left gap = X Ω, Resistance in right gap = Y Ω, l = 30 cm and, 100 – l = 100 – 30 = 70 cm
For balanced metre bridge

∴ X/Y = 30/70
∴ X = (3/7)Y ………. (1)
Case – II:
Given: Y is shunted by 15 Ω, resistance in left gap = X Ω, Resistance in right gap = (15 x Y)/(15 + Y)
As Y is shunted, the resultant resistance reduces thus the null point shifts towards the right by 10 cm
l = 40 cm and, 100 – l = 100 – 40 = 60 cm
For balanced metre bridge

∴ 45 + 3Y = 70
∴ 3Y = 25
∴ Y = 25/3 Ω
X = (3/7)Y = (3/7) x (25/3) = 25/7 Ω
Ans: X = 25/7 Ω and Y = 25/3 Ω
Example – 07:
With two resistances in two gaps of a metre bridge, the null point is at 0.4 m from zero end. When 10 Ω resistance coil is put in series with smaller resistance the null point is at 0.6 m from the same end. Find the resistances.
Solution:
Case – I:
Given: Resistance in left gap = X Ω, Resistance in right gap = Y Ω, l = 0.4 m = 40 cm and, 100 – l = 100 – 40 = 60 cm
For balanced metre bridge

∴ X/Y = 40/60
∴ Y = (3/2)X ………. (1)
Case – II:
Y = (3/2)X Thus X < Y. Thus 10 Ω resistance is connected in series with X.
X is shunted by 10 Ω, resistance in the left gap = (X + 10) Ω, Resistance in right gap = Y, l = 0.6 m = 60 cm and, 100 – l = 100 – 60 = 40 cm
For balanced metre bridge

∴ 4X + 40 = 9X
∴ 5X = 40
∴ X = 8 Ω
Y = (3/2)X = (3/2) x 8 = 12 Ω
Ans: The two resistances are 8 Ω and 12 Ω
Example – 08:
Two resistances X and Y are connected in the left and right gap of metre bridge. The null point is measured from the left end and the ratio of balancing lengths is found to be 2:3. If the value of X is changed by 20 Ω, the ratio of balancing lengths measure from the left end of the wire is found to be 1:4. Find X and Y.
Solution:
Case – I:
Given: Resistance in left gap = X Ω, Resistance in right gap = Y Ω, l : (100 – l ) = 2:3
For balanced metre bridge

∴ X/Y = 2/3
∴ X = (2/3)Y ………. (1)
Case – II:
Given: The value of X is changed by 20 Ω. now new ratio of length (1:4) is less than the ratio of lengths in case – I (2:3). It means value of X is reduced. resistance in left gap = (X – 20) Ω, Resistance in right gap = Y Ω.
l : (100 – l ) = 1:4
For balanced metre bridge

∴ (X – 20)/Y = 1/4
∴ X – 20 = (1/4)Y
∴ (2/3)Y – 20 = (1/4)Y
∴ (2/3)Y – (1/4)Y = 20
∴ (5/12)Y = 20
∴ Y = 48 Ω
∴ X = (2/3)Y = (2/3) x 48 = 32 Ω
Ans: X = 32 Ω and Y = 48 Ω
Example – 09:
Two resistances X and Y in the two gaps of a Wheatstone’s metre bridge give a null point dividing the wire in the ratio 2: 3. If each resistance is increased by 30 Ω, the null point divides the wire in the ratio 5:6. Calculate each resistance.
Solution:
Case – I:
Given: Resistance in left gap = X, Resistance in right gap = Y
l /(100 – l )= 2/3
For balanced metre bridge

∴ X/Y = 2/3
∴ X = (2/3)Y ………. (1)
Case – II:
Given: Resistance in left gap = X+ 30 Ω Resistance in right gap = Y+ 30 Ω
l /(100 – l )= 5/6
For balanced metre bridge

∴ (X+ 30)/(Y + 30) = 5/6
∴ 6X + 180 = 5Y + 150
∴ 5Y – 6 X = 30
∴ 5Y – 6 x (2/3)Y = 30
∴ 5Y – 4Y = 30
∴ Y = 30 Ω
X = (2/3)Y = (2/3) x 30 = 20 Ω
Ans: X = 20 Ω and Y = 30 Ω
Example – 10:
A unknown resistance X is connected in a left gap and known resistance R is connected in the right gap of metre bridge. The balance point is obtained at 60 cm from the left end of wire. When R is increased by 2 Ω, the balance point shifts 10 cm. Find X and R
Solution:
Case – I:
Given: Resistance in left gap = X Ω, Resistance in right gap = R Ω, l = 60 cm and, 100 – l = 100 – 60 = 40 cm
For balanced metre bridge

∴ X/R = 60/40
∴ X = (3/2)R ………. (1)
Case – II:
Given: The value of R is increased by 2 Ω. The balance point should shift towards right. l = 50 cm and, 100 – l = 100 – 50 = 50 cm
For balanced metre bridge

∴ X/(R + 2) = 50/50
∴ X/(R + 2) = 1
∴ X = R + 2
∴ (3/2)R = R + 2
∴ (3/2)R – R = 2
∴ (1/2)R = 2
∴ R = 4 Ω
X = (3/2)R = (3/2) x 4 = 6 Ω
Ans: X = 6 Ω and R = 4 Ω
Example – 11:
In a metre bridge experiment, with the resistance R1 in the left gap and a resistance X in the right gap, the null point is obtained at 40 cm from the left end. With the resistance R2 in the left gap and the same resistance X in the right gap, the null point is obtained at 50 cm from the left end. Where will be the null point if R1 and R2 are put series in the left gap and the right gap still containing X?
Solution:
Case – I:
Given: Resistance in left gap = R1, Resistance in right gap = X, l = 40 cm and, 100 – l = 100 – 40 = 60 cm
For balanced metre bridge

∴ R1/X = 40/60
∴ ∴ R1 = (2/3) X ………. (1)
Case – II:
Given: Resistance in left gap = R2, Resistance in right gap = X, l = 50 cm and, 100 – l = 100 – 50 = 50 cm
For balanced metre bridge

∴ R2/X = 50/50
∴ R2 = X ………. (2)
Case – III:
Given: Resistance in left gap = R1 + R2 , Resistance in right gap = X
Let l be the distance of the null point from the left end.
For balanced metre bridge

∴ (R1 + R2)/X = l / (100 – l)
∴ (2/3 X + X)/X = l / (100 – l)
∴ (5/3 X) /X = l / (100 – l)
∴ 5/3 = l / (100 – l)
∴ 500 – 5l= 3l
∴ 8l = 500
∴ l = 500/8 = 62.5 cm
Ans: The null point is at 62.5 cm on the wire from the left end.
Example – 12:
In a metre bridge experiment, with the resistance R1 in the left gap and a resistance X in the right gap, the null point is obtained at 40 cm from the left end. With the resistance R2 in the left gap and the same resistance X in the right gap, the null point is obtained at 50 cm from the left end. Where will be the null point if R1 and R2 are put parallel in the left gap and the right gap still containing X?
Solution:
Case – I:
Given: resistance in left gap = R1, Resistance in right gap = X. l = 40 cm and, 100 – l = 100 – 40 = 60 cm
For balanced metre bridge

∴ R1/X = 40/60
∴ ∴ R1 = (2/3) X ………. (1)
Case – II:
Given: resistance in left gap = R2, Resistance in right gap = X, l = 50 cm and, 100 – l = 100 – 50 = 50 cm
For balanced metre bridge

∴ R2/X = 50/50
∴ R2 = X ………. (2)
Case – III:

Resistance in right gap = X
Let l be the distance of the null point from the left end.
For balanced metre bridge

∴ (2/5)X/X = l / (100 – l)
∴ 2/5= l / (100 – l)
∴ 2(100 – l)= 5l
∴ 200 – 2l= 5l
∴ 7l = 200
∴ l = 200/7 = 28.57 cm
Ans: The null point is at 28.57 cm on the wire from the left end.
Example – 13:
With a coil of unknown resistance X in the left gap and resistance R in the right gap of a metre bridge, the null point is obtained at 40 cm from the left end. When resistance of 10 Ω is put in series with X, the null point is at the centre of the wire with R still in the right gap. Find X and R. Where would the null point be if the 10 Ω resistance is put in parallel with X and R still in the right gap.
Solution:
Case – I:
Given: resistance in left gap = X, Resistance in right gap = R, l = 40 cm and, 100 – l = 100 – 40 = 60 cm
For balanced metre bridge

∴ X/R = 40/60
∴ X = (2/3) R ………. (1)
Case – II:
Given: a resistance of 10 Ω is put in series with X. resistance in left gap = X + 10, Resistance in right gap = R, l = 50 cm and, 100 – l = 100 – 50 = 50 cm
For balanced metre bridge

∴ (X + 10)/R = 50/50 = 1
∴ X + 10 = R
∴ (2/3) R + 10 = R
∴ 10 = R – (2/3) R
∴ 10 = (1/3) R
∴ R = 30 Ω
X = (2/3) R = (2/3) x 30 = 20 Ω
Case – III:
Given: 10 Ω resistance is connected in parallel with X.
resistance in left gap = 10X/(X + 10) = (10 x 20)/(10 + 20) = 200/30 = (20/3) Ω, Resistance in right gap = R
Let l cm be the distance of null point from left end.
For balanced metre bridge

∴ (20/3)/30 = l / (100 – l)
∴ 20/90 = l / (100 – l)
∴ 2/9 = l / (100 – l)
∴ 200 – 2l = 9l
∴ 11l = 200
∴ l = 200/11 = 18.2 cm
Ans: X = 20 Ω, R = 30Ω and the required balance point at 18.2 cm from left end of wire.
Example – 14:
With an unknown resistance X in the left gap and a resistance of 30 Ω in the right gap of the metre bridge the null point is obtained at 40 cm from the left end of the wire. Find (i) the unknown resistance and (ii) the shift in the position of the null point a) when the resistance in both the gaps are increased by 15 Ω and b) when the resistances in each gap is shunted by 8 Ω.
Solution:
Part (i)
resistance in left gap = X Ω, Resistance in right gap = 30 Ω
l = 40 cm and, 100 – l = 100 – 40 = 60 cm
For balanced metre bridge

∴ X/30 = 40 / 60 = 2/3
∴ X = 20 Ω
Case a) when the resistance in both the gaps are increased by 15 Ω
resistance in left gap = X + 15 = 20 + 15 = 35 Ω, Resistance in right gap = 30 + 15 = 45 Ω
Let l cm be the distance of null point from left end.
For balanced metre bridge

∴ (20/3)/30 = l / (100 – l)
∴ 35/45 = l / (100 – l)
∴ 7/9 = l / (100 – l)
∴ 700 – 7l = 9l
∴ 16l = 700
∴ l = 700/16 = 43.75 cm
Shift in null point = 43.75 – 40 = 3.75 cm towards right
Case b) when the resistances in each gap is shunted by 8 Ω.
Resistance in left gap = (20 x 8)/(20 + 8) = 160/28 = 40/7 Ω,
Resistance in right gap = (30 x 8)/(30 + 8) = 240/38 = 120/19
Let l cm be the distance of null point from left end.
For balanced metre bridge

∴ (40/7)/(120/19) = l / (100 – l)
∴ (1/7)/(3/19) = l / (100 – l)
∴ ∴ (19/21) = l / (100 – l)
∴ 1900 – 19l = 21l
∴ 40l = 1900
∴ l = 1900/40 = 47.5 cm
Shift in null point = 47.5 – 40 = 7.5 cm towards right
Previous Topic: Kirchhoff’s Laws
Next Topic: More Problems on Metre Bridge