Numerical Problems on Stress, Strain, and Young’s Modulus

Science > Physics > Elasticity > Numerical Problems on Stress, Strain, and Young’s Modulus

In this article, we shall study concept application and numerical problems on longitudinal stress, longitudinal strain, Young’s modulus of elasticity.

Conversion Factors:

From	To	Factor
mm	m	x 10-3
cm	m	x 10-2
m	mm	x 103
m	cm	x 102
dyne	N	x 10-5
N	dyne	x 105
cm2	m2	x 10-4
m2	cm2	x 104
kPa	Pa	x 103
MPa	Pa	x 106
GPa	Pa	x 109

Formulae:

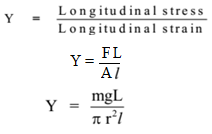
Example – 1:

A wire 2 m long and 2 mm in diameter, when stretched by weight of 8 kg has its length increased by 0.24 mm. Find the stress, strain and Young’s modulus of the material of the wire. g = 9.8 m/s²

Given: Initial length of wire = L = 2 m, Diameter of wire = 2 mm, Radius of wire 2/2 = 1 mm = 1 × 10^-3 m, Weight attached = m = 2 kg, Increase in length = l = 0.24 mm = 0.24 × 10^-3 m, g = 9.8 m/s².

To Find: Stress =? Strain =? Young’s modulus of material = Y =?

Solution:

Stress = F / A  = mg /π r²
∴  Stress =  ( 8 × 9.8) /(3.142 ×(1 × 10^-3)²)
∴  Stress =  ( 8 × 9.8) /(3.142 ×  1 × 10^-6)
∴  Stress =  2.5× 10⁷ N/m²
Strain = l / L =   0.24 × 10^-3 / 2
∴ Strain =0.12 × 10^-3 =1.2 × 10^-4
Now, Young’s modulus of elasticity= Y = Stress / Strain

∴ Y = (2.5× 10⁷) / (1.2 × 10^-4)
∴ Y = 2.08 × 10¹¹ N/m²
Ans.: Stress =  2.5× 10⁷ N/m², Strain  =1.2 × 10^-4 ,  Yong’s modulus of elasticity= 2.08 × 10¹¹ N/m²

Example – 2:

A wire of length 2 m and cross-sectional area 10^-4 m² is stretched by a load 102 kg. The wire is stretched by 0.1 cm. Calculate longitudinal stress, longitudinal strain and Young’s modulus of the material of wire.

Given: Initial length of wire = L = 2 m, Cross-sectional area = A = 10^-4 m, Stretching weight = 102 kg wt = 102 × 9.8 N, Increase in length = l = 0.1 cm = 0.1 × 10^-2 m = 1 × 10^-3 m, g = 9.8 m/s².

To Find: Stress =? Strain = ?, Young’s modulus of material = Y = ?

Solution:

Stress = F / A  = mg /A
∴  Stress =  ( 102 × 9.8) /10^-4
∴  Stress =  1 × 10⁷ N/m²
Strain = l / L =   1 × 10^-3 / 2
∴  Strain = 0.5 × 10^-3 = 5 × 10^-4
Now, Young’s modulus of elasticity= Y = Stress / Strain = (1 × 10⁷) / ( 5 × 10^-4)
∴  Y = 2 × 10¹⁰ N/m²
Ans.: Stress =  1 × 10⁷ N/m², Strain = 5 × 10^-4 , Young’s modulus of elasticity= Y = 2 × 10¹⁰ N/m²

Example – 3:

A mild steel wire of radius 0.5 mm and length 3 m is stretched by a force of 49 N. calculate a) longitudinal stress, b) longitudinal strain c) elongation produced in the body if Y for steel is 2.1 × 10¹¹ N/m².

Given: Initial length of wire = L = 3 m, radius of wire = 0.5 mm = 0.5 × 10^-3 m = 5 × 10^-4 m,Force applied =49 N, Young’s modulus for steel = Y = 2.1 × 10¹¹ N/m².

To Find: Stress =? Strain =? elongation =?

Solution:

Stress = F / A  = mg /π r²
∴  Stress =  49 /(3.142 ×(5 × 10^-4)²)
∴  Stress = 49 /(3.142 × 25 × 10^-8)
∴  Stress = 6.238 × 10⁷ N/m²
Now, Y = Stress / Strain
∴  Strain = Stress / Y =  (6.238 × 10⁷ ) / (2.1 × 10¹¹)
∴  Strain = 2.970 × 10^-4
Now, Strain = l / L
∴ l = Strain  × L
∴  l = 2.970 × 10^-4  × 3
∴  l = 8.91 × 10^-4  m = 0. 891 × 10^-3 m = 0.891 mm
Ans.: Stress = 6.238 × 10⁷ N/m², Strain = 2.970 × 10^-4, Elongation = 0.891 mm.

Example – 4:

A metal wire 1 m long and of 2 mm diameter is stretched by a load of 40 kg. If Y = 7 × 10¹⁰ N/m² for the metal, find the (1) stress (2) strain and (3) force constant of the material of the wire.

Given: Initial length of wire = L = 1 m, Diameter of wire = 2 mm, Radius of wire = 2/2 = 1 mm = 1 × 10^-3 m, Load attached = m = 40 kg, Young’s modulus of material = Y = 7 × 10¹⁰ N/m².

To Find: Stress =? Strain = ?, Force constant = ?

Solution:

Stress = F / A  = mg /π r²
∴  Stress =  ( 40 × 9.8) /(3.142 ×(1 × 10^-3)²)
∴  Stress =  ( 40 × 9.8) /(3.142 ×  1 × 10^-6)
∴  Stress =  1.25 × 10⁸    N/m²
Now, Y = Stress / Strain
∴   Strain = Stress / Y  =  1.25 × 10⁸  / 7 × 10¹⁰
∴   Strain = 1.78 × 10^-3
Now, Strain = l /L
∴ extension = l = Strain × L
∴  l = 1.78 × 10^-3 × 1
∴  l = 1.78 × 10^-3 m
Now, force constant K = F/l = mg/l = ( 40 × 9.8) /(1.78 × 10^-3)
∴  Force constant K = 2.2 × 10⁵  N/m
Ans.: Stress =  1.25 × 10⁸    N/m²,  Strain = 1.78 × 10^-3,  Force constant = 2.2 × 10⁵  N/m

Example – 5:

What must be the elongation of a wire 5m long so that the strain is 1% of 0.1? If the wire has cross-selection of 1mm² and is stretched by 10 kg-wt, what is the stress?

Given: Initial length of wire = L = 5 m, Strain = 1% of 0.1 = 1 × 10^-2 × 0.1 = 1 × 10^-3, Area of cross-section = 1 mm² =  1 × 10^-6 m², Load attached = F = 10 kg-wt = 10 × 9.8 N .

To Find: Elongation = l =? Stress = ?,

Solution:

Strain = l /L
∴ extension = l = Strain × L
∴  l = 1 × 10^-3 × 5
∴  l = 5 × 10^-3 m = 5 mm
Stress = F / A  = mg /π r²
∴  Stress =  ( 10 × 9.8) /( 1 × 10^-6 )
∴  Stress =  9.8 × 10⁷    N/m²
Ans.: Extension = 5 mm and Stress =  9.8 × 10⁷    N/m²

Example-6:

A brass wire of length 2 m has its one end, fixed to a rigid support and from the other end a 4 kg wt is suspended. If the radius of the wire is 0.35 mm, find the extension produced in the wire.  g = 9.8 m/s², Y = 11 × 10¹⁰ N/m²

Given: Initial length of wire = L = 2 m, Radius of wire = 0.35 mm = 0.35 × 10^-3 m = 3.5 × 10^-4 m, Load attached = F = 4 kg wt = 4 × 9.8 N, g = 9.81 m/s², Y = 11 × 10¹⁰ N/m².

To Find: Extension =?

Solution:

Y = FL /A l
∴  l = F L /π r² Y
∴  l = (4 × 9.8  × 2) /(3.142 × (3.5 × 10^-4)² × 11 × 10¹⁰ )
∴  l = (4 × 9.8  × 2) /(3.142 × 12.25 × 10^-8 × 11 × 10¹⁰ )
∴  l = 1.85 × 10^-3 m =  0.185 × 10^-2 m = 0.185 cm
Ans.: Extension of wire is 0.185 m

Example-7:

A wire of length 1.5 m and of radius 0.4 mm is stretched by 1.2 mm on loading. If the Young’s modulus of its material is 12.5 × 10¹⁰ N/m². , find the stretching force.

Given: Initial length of wire = L = 1.5 m, Radius of wire = 0.4 mm = 0.4 × 10^-3 m = 4 × 10^-4 m, Extension = l = 1.2 mm = 1.2 × 10^-3 m, g = 9.8 m/s², Young’s modulus = Y = 12.5 × 10¹⁰ N/m².

To Find: Stretching force = F =?

Solution:

Y = FL /A l
∴  F = AY l /L
∴  F = π r² Y l /L
∴  F = (3.142 × (4 × 10^-4)² × 12.5 × 10¹⁰ × 1.2 × 10^-3) /1.5
∴  F = (3.142 × 16 × 10^-8 × 12.5 × 10¹⁰ × 1.2 × 10^-3) /1.5
∴  F = 50.27 N
Ans.: Stretching force required = 50.27 N

Example – 8:

What force is required to stretch a steel wire 1 cm2 in cross-section to double its length? Y = 2× 10¹¹ N/m². Assume Hooke’s law.

Given: Initial length of wire = L, Final length = 2L, Hence extension of wire = l = 2L – L = L, Area of cross-section = 1 cm² =  1 × 10^-4 m², Young’s modulus of elasticity =  Y = 2× 10¹¹ N/m².

To Find: Stretching force = F =?

Solution:

Y = FL /A l
∴ F = AY l /L
∴ F = (1 × 10^-4 × 2× 10¹¹ × L) /L
∴ F =2 × 10⁷
Ans.: Stretching force required = 2 × 10⁷ N

Example – 9:

Find the maximum load which may be placed on a tungsten wire of diameter 2 mm so that the permitted strain not exceed 1/1000. Young’s modulus for tungsten = Y = 35 × 10¹⁰ N/m².

Given:  Strain = 1/1000 = 10^-3, Young’s modulus of elasticity = Y = 35 × 10¹⁰ N/m², Diameter of wire = 2 mm, Radius of wire = 2/2 = 1 mm = 1 × 10^-3 m,

To Find: Maximum load = F =?

Solution:

Y = Stress /Strain = (F/A)/Strain
Y = F/(A × strain)
∴  F = π r² × Y× strain
∴  F = 3.142  × (1 × 10^-3)² × 35 × 10¹⁰× 10^-3
∴  F = 3.142  × 1 × 10^-6 × 35 × 10¹⁰× 10^-3
∴  F = 1100 N
Ans.: Maximum load can be placed is 1100 N

Problem – 10:

A mass of 2kg is hung from a steel wire of radius 0.5 mm and length 3m. Compute the extension produced. What should be the minimum radius of wire so that elastic limit is not exceeded? Elastic limit for steel is 2.4 × 10⁸ N/m², Y for steel = Y = 20 × 10¹⁰ N/m²

Given:  Radius of wire = 0.5 mm = 0.5 × 10^-3 m = 5 × 10^-4 m. Initial length of wire = L = 3m, Mass attached = m = 2 kg, Y for steel = Y = 20 × 10¹⁰ N/m²

To Find: Extension = l =?, Minimum radius of wire = r =?

Solution:

Part – I:

Y= F L /A l
∴  l = F L /A Y
∴  l = m g L /π r² Y
∴  l = (2 × 9.8  × 3) /(3.142 1 × (5× 10^-4)²× 20 × 10¹⁰ )
∴  l = (2 × 9.8  × 3) /(3.142  × 25× 10^-8 × 20 × 10¹⁰ )
∴  l = 3.743 × 10^-4 m = 0.3743 mm

Part – II:

Given:  Elastic limit for steel = Stress = 2.4 × 10⁸ N/m², Mass attached = m = 2 kg,

To Find: Radius of wire at elastic limit = r =?

Stress = F /A = F /π r²
∴   r² = mg / (π × Stress)
∴   r² = (2 × 9.8)  / (3.142 × 2.4 × 10⁸)
∴   r² = 2.599× 10^-8
∴   r = 1.612× 10^-4  m = 0.1612× 10^-3 m =  0.1612 mm

Ans.: Part – I:Change in length of wire is  0.3743 mm
Part – II: Radius of wire at elastic limit = 0.1612 mm

Example – 11:

A wire is stretched by the application of a force of 50 kg wt/sq. cm. What is the percentage increase in the length of the wire? Y = 7 × 10¹⁰ N/m², g = 9.8 m/s²

Given:  Stress = 50 kg wt/sq. cm = 50 × 9.8 N / 10^-4 m² = 50 × 9.8 × 10⁴ N/m², Young’s modulus of elasticity = Y = 7 × 10¹⁰ N/m². g = 9.8 m/s²

To Find: % elongation = % l/L =?

Solution:

Now, Y = Stress / Strain
∴   Strain = Stress / Y = (50 × 9.8 × 10⁴)/ (7 × 10¹⁰)
∴   Strain = 7 × 10^-5
% elongation = Strain × 100 =  7 × 10^-5  × 100
% elongation = Strain × 100 =  0.007
Ans.: Elongation is 0.007 percent

Problem – 12:

A compressive force of 4 × 10⁴ N is exerted at the end of a bone of length 30 cm and 4 cm² square cross-sectional area. What will happen to the bone? Calculate the change in length of a bone. Compressive strength of bone is 7.7 × 10⁸ N/m² and Young’s modulus of bone is 1.5 × 10¹⁰ N/m²

Given: Initial length of wire = L = 30 cm = 0.30 m, Area of cross-section = 4 cm² =  4× 10^-4 m², Load attached = F = 4 × 10⁴ N . Y = 1.5 × 10¹⁰ N/m². Maximum Stress = 7.7 × 10⁸ N/m².

To Find: Effect of loading =? Change in length = l = ?,

Solution:

Applied Stress = Applied force / Area of cross-section
Applied Stress = (4 × 10⁴ )/ (4× 10^-4 ) =  1 × 10⁸ N/m²
This stress is less than the maximum allowable stress (7.7 × 10⁸ N/m²)
Hence the bone will not break but will get compressed and its length decreases
Y= F L /A l
∴  l = (4 × 10⁴ × 0.3) /(4× 10^-4  × 1.5 × 10¹⁰)
∴  l = 2 × 10^-3 m = 2 mm
Ans.: The length of bone decreases by 2 mm

Example – 13:

The radius of a copper bar is 4 mm. What force is required to stretch the rod by 20% of its length assuming that the elastic limit is not exceeded?  Y = 12 × 10¹⁰ N/m².

Given: Radius of wire = r = 4 mm = 4 × 10^-3 m, % elongation = Strain = 20% = 20 × 10^-2, Young’s modulus of elasticity = Y = 12× 10¹⁰ N/m².

To Find: Stretching force = F =?

Solution:

Y = Stress /Strain = (F/A)/Strain
Y = F/(A × strain)
∴  F = AY× strain
∴  F = π r² × Y × strain
∴  F = 3.142  × (4 × 10^-3)² × 12× 10¹⁰ × 20 × 10^-2
∴  F = 3.142  × 16 × 10^-6 × 12× 10¹⁰ × 20 × 10^-2
∴  F = 1.207× 10⁶ N
Ans.: Stretching force required = 1.207× 10⁶ N

Example – 14:

Find the change in length of a wire 5m long and 1 mm² in cross-section when the stretching force is 10 kg-wt. Y = 4.9 × 10¹¹ N/m², and g=9.8 m/s².

• Solution:
• Given: Initial length of wire = L = 5 m, Area of cross-section = 1 mm² = 1 × 10^-6 m², Load attached = F = 10 kg-wt = 10 × 9.8 N . Y = 4.9 × 10¹¹ N/m², and g=9.8 m/s².
• To Find: Change in length = l =?

Y = FL /A l
∴ l = F L /A Y
∴ l = (10 × 9.8 × 5) / (1 × 10^-6 × 4.9 × 10¹¹)
∴  l = 1 × 10^-3 m = 1 mm
Ans.: Change in length of wire is  1 mm

Example – 15:

Elastic limit is exceeded when the strain in a wire (Y=14 × 10¹¹ N/m²) exceeds 1/2000. If the area of the cross-section of the wire is 0.02 cm², find the maximum load that can be used for stretching the wire without causing a permanent set.

Given:  Strain = 1/2000 = 5 × 10^-4, Young’s modulus of elasticity =  Y = 14 × 10¹¹ N/m², Area of cross section = A = 0.02 cm² = 0.02 × 10^-4 m² = 2 × 10^-6 m²

To Find: Stretching force = F =?

Solution:

Y = Stress /Strain = (F/A)/Strain
Y = F/(A × strain)
∴  F = AY× strain
∴  F = 2 × 10^-6 × 14 × 10¹¹ × 5 × 10^-4
∴  F = 1400 N
Ans.: Stretching force required = 1400 N

Example – 16:

Elastic limit of steel is exceeded when the stress on given steel wire exceeds 8.26 × 10⁸ N/m². Can a steel wire (Y = 2 × 10¹¹ N/m²) 2m long be stretched by 10 mm without exceeding the elastic limit?

Given: Initial length of wire = L = 2 m, Elastic limit = stress = 8.26 × 10⁸ N/m², Young’s modulus of elasticity = Y = 2 × 10¹¹ N/m².

To Find: To find whether wire can be stretched by 10 mm.

Solution:

Y = Stress /Strain = Stress/(l/L)
∴  Y    = (Stress × L) / Y
∴  Y = (8.26 × 10⁸ × 2) / 2 × 10¹¹
∴  Y = 8.26 × 10^-3  m  = 8.26 mm
Ans.: Wire cannot be stretched up to 10 mm because the elastic limit will get crossed at extension of 8.26 mm.

Example – 17:

Young’s modulus of the material of a wire is 9.68 × 10¹⁰ N/m². A wire of this material of diameter 0.95 mm is stretched by applying a certain force. What should be the limit of this force if the strain is not to exceed 1 in 1000?

Given:  Strain = 1/1000 = 10^-3 , Young’s modulus of elasticity =  Y = 9.68 × 10¹⁰ N/m², Diameter of wire = 0.95 mm, Radius of wire = 0.95/2 = 0.475 mm = 0.475 × 10^-3 m =  4.75 × 10^-4 m

To Find: Stretching force = F =?

Solution:

Y = Stress /Strain = (F/A)/Strain
Y = F / (A × strain)
∴  F = π r² × Y× strain
∴  F = 3.142  × (4.75 × 10^-4)² × 9.68 × 10¹⁰× 10^-3
∴  F = 68.62
Ans.: Limit of the stretching force required = 68.62 N

Example – 18:

The elastic limit of copper is 1.5 × 10⁸ N/m². A copper wire is to be stretched by a load of 10 kg. Find the minimum diameter the wire must have if the elastic limit is not to be exceeded.

Given: Elastic Limit = Stress = 1.5 × 10⁸ N/m², Load = F = 10 kg wt = 10 × 9.8.

To Find: Minimum diameter of the wire.

Solution:

Stress = F / A
∴  Stress = F / π r²
∴  r²  = F / (π × Stress )
∴  r²  = (10 × 9,8) / (3.142 × 1.5 × 10⁸ )
∴  r²  = 20.79 × 10^-8
∴  r  = 4.56 × 10^-4   m = 0.456 × 10^-3   m = 0.456 mm
Diameter of wire = 2 × r = 2 × 0.456 mm =0.912 mm
Ans.: Diameter of wire is 0.912 mm

Example – 19:

What would be the greatest length of a steel wire which when fixed at one end can hang freely without breaking? Density of steel = 7800 kg/m³. Breaking stress for steel = 7.8 × 10⁸ N/m².

Given: Density of steel = ρ = 7800 kg/m³. Stress = 7.8 × 10⁸ N/m².

To Find: Greatest length of the wire =?.

Solution:

Stress = F / A   = mg / A =  V ρ g /A
∴ Stress =   A L  ρ g / A
∴ Stress =   L  ρ g
∴ L = Stress /  ρ g
∴ L = 7.8 × 10⁸ /  (7800 × 9.8)
∴ L = 7.8 × 10⁸ /  (7800 × 9.8)
∴ L = 1.021 × 10⁴   m
Ans.: Maximum length of copper wire is  1.021 × 10⁴   m

For More Topics in Elasticity Click Here

For More Topics in Physics Click Here