Science > Chemistry > Concept of Atomic Mass and Equivalent Mass > Hydrogen Displacement Method
In the last few articles, we have studied the concept of atomic mass and methods to determine it. In this article, we shall study the hydrogen displacement method to determine the equivalent mass of a metal.
The equivalent mass of a substance is the number of parts by mass of the substance which combines with or displaces or contains 1.008 parts by mass of hydrogen, 8 part by mass of oxygen, or 35.5 part by mass of chlorine. If the equivalent mass is expressed in grams then it is called gram equivalent mass (GEM).
Illustration:
1.008 parts by weight of Hydrogen combines with 35.5 parts by weight of chlorine to give 36.5 parts by weight of HCI. Thus the equivalent mass of chlorine is 35.5.
Equivalent mass has no unit because it is a pure ratio. Some important equivalent masses are H = 1, O = 8, Cl = 35.5
Hydrogen Displacement Method:
Principle:
The known mass of a metal to react with dilute acids and volume of hydrogen produced in the reaction is measured and the equivalent mass of an element is calculated using formula
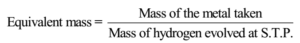
This method is useful for the metals which react, or dissolves in mineral acids and liberates hydrogen gas. e.g. Mg, Zn, Al, Ca, Zn, Sn etc.
Procedure:
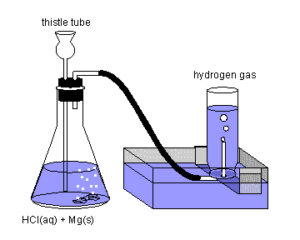
Clean and weigh accurately a piece of metal (Mg / Zn / Al) whose equivalent mass is to be found and place it in a conical flask containing distilled water.
The mouth of the conical flask is fitted with a cork through which side tube (gas carrying tube) and a thistle tube are inserted as shown in the diagram. Using side tube the conical flask is connected to graduated (calibrated) test tube called Eudiometer. Eudiometer tube is completely filled with water and is inverted on the side tube as shown in the diagram. The bottom part of thistle tube is dipped in the water in the flask. Mineral acid like HCl is added to the flask through the thistle funnel.
The reaction between the metal and acid takes place and hydrogen gas is liberated which is collected in eudiometer by downward displacement of water.
When the evolution of gas has stopped the mouth of the eudiometer tube is closed with a thumb and carried to a tray of water where the level of water inside and outside the tube is equalised and the volume of hydrogen gas is read at atmospheric pressure.
Observations:
The weight of metal piece = W g
The volume of hydrogen collected = V dm³
Atmospheric pressure = P mm of Hg
Aqueous tension = f mm of Hg
Room temperature = t °C
Absolute temperature = T K
Calculations:
Now the volume of hydrogen at S.T.P. from the above data using following formula is calculated.

Where Volume of hydrogen at S.T.P. Vo dm³,
Pressure at S.T.P. Po mm of Hg = 760 mm = 1.013 x 105 N/m2
The absolute temperature at S.T.P. To K = 273 K

Notes:
- Hydrogen is collected over water and it is moist. Hence, the pressure of hydrogen = (P – f) mm of Hg is used.
- This method does not give accurate results.
Numerical Problems
Example – 01:
0.205 g of a metal on treatment with a dil. acid gave 106.6 ml of hydrogen collected over water at 755 mm pressure and 17 °C. Calculate the equivalent mass of the metal if aqueous tension at 17 °C is 14.4 mm.
Given: W = 0.205 g, V = 106.6 ml, P = 755 mm of Hg, f = 14.4 mm of Hg, (P – f) = 755 – 14.4 = 740.6 mm of Hg, t = 17 °C, T = 17 + 273 = 290 K, Po = 760 mm of Hg, To = 273 K.
Solution:

Ans: the equivalent mass of the metal is 23.5
Example – 02:
0.33 g of metal on dissolving in dilute sulphuric acid, liberates 113 ml of dry hydrogen at NTP. Determine the equivalent mass of the metal.
Given: W = 0.33 g, Vo = 113 ml = 0.113 dm³
Solution:

Ans: the equivalent mass of the metal is 32.71
Example – 03:
0.05 g of metal on treatment with a dilute acid gave 51 ml of hydrogen collected over water at 751 mm pressure and 27 °C. Calculate the equivalent mass of the metal.
Given: W = 0.05 g, V = 51 ml, P = 751 mm of Hg, f = 0 (not mentioned in problem), P – f = P, t = 27 °C, T = 27 + 273 = 300 K, Po = 760 mm of Hg, To = 273 K
Solution:

Ans: the equivalent mass of the metal is 12.21
Example – 04:
0.0396 g of metal was completely dissolved in dilute hydrochloric acid and hydrogen evolved is mixed with dry oxygen. Then the mixture is sparked. 13.75 ml of dry oxygen at 27 °C and 680 mm pressure is required for complete combustion of oxygen formed. Find the equivalent mass of the metal.
Given: W = 0.0396 g, P = 680 mm of Hg, f = 0 (not mentione), t = 27O C, T = 27 + 273 = 300 K, Po = 760 mm of Hg, To = 273 K
Solution:
Combustion of hydrogen is represented as
2 H2(g) + O2(g) → 2H2O(g))
2 vol 1 vol 2 vol
Thus 1vol of oxygen combines with 2 vol of hydrogen.
Using Gay-Lussac’s law of combining volume we can say that
13.75 ml of oxygen combines with 2 x 13.75 = 27.5 ml of hydrogen.
∴ V = 27.5 ml

Ans: the equivalent mass of the metal is 19.80
In the next article, we shall study oxide formation method, reduction method, and chloride formation method to determine equivalent mass.
Previous Topic: Atomic Mass by Dulong Petit’s Law
Next Topic: Equivalent Mass by Oxide formation, Chloride Formation, and Reduction Method