Numerical Problems on Density of Solid

Science > Chemistry > Solid State > Numerical Problems on Density of Solid

In this article, we shall study to solve numerical problems to find the density of solid, edge length and volume of the unit cell.

Example – 01:

Silver crystallizes in face centred cubic structure. The edge length of a unit cell is found to be 408.7 pm. Calculate the density of silver. (Ag = 108 g mol^-1)

Given: The edge length of the unit cell = a = 408.7 pm = 408.7 x 10^-10cm, Atomic mass of silver = M = 108 g mol^-1, Avogadro’s number N = 6.022 x 10²³ mol^-1. Type of crystal structure = face centred cubic

To Find: Density of silver =?

Solution:

The number of atoms in the unit cell of a face centred cubic structure is n = 4

Ans: Density of silver is 10.51 g/cm³

Example – 02:

Copper crystallizes in face centred cubic structure. The edge length of a unit cell is found to be 3.61 x 10^-8 cm. Calculate the density of copper if the molar mass of copper is 63.5 g mol^-1

Given: The edge length of the unit cell = a = 3.61 x 10^-8 cm, molar mass of copper = M = 63.5 g mol^-1, Avogadro’s number N = 6.022 x 10²³ mol^-1. Type of crystal structure = face centred cubic

To Find: Density of copper =?

Solution:

The number of atoms in the unit cell of a face centred cubic structure is n = 4

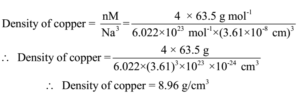
Ans: Density of copper is 8.96 g/cm³

Example – 03:

Determine the density of caesium chloride which crystallizes in bcc type structure with an edge length of 412.1 pm. The atomic mass of Cs and Cl are 133 and 35.5 respectively.

Given: The edge length of the unit cell = a = 412.1 pm = 412.1 x 10^-10 cm, atomic mass of Cs = 133, atomic mass of Cl = 35.5, Avogadro’s number N = 6.022 x 10²³ mol^-1. Type of crystal structure = bcc

To Find: Density of caesium chloride =?

Solution:

Volume of unit cell = a³ = (4.121 x 10^-8 cm) ³ = (4.121) ³ x 10^-24 cm³.

Mass of one atom of Cs = Atomic mass of Cs / Avogadro’s number

Mass of one atom of Cs = 133 g mol^-1 / 6.022 x 10²³ mol^-1

Mass of one atom of Cs = 22.09 x 10^-23 g

Mass of one atom of Cl = Atomic mass of Cl / Avogadro’s number

Mass of one atom of Cl = 35.5 g mol^-1 / 6.022 x 10²³   mol^-1

Mass of one atom of Cl = 5.894 x 10^-23 g

Caesium chloride has a body-centred cubic structure such that caesium atom is at centre

and eight chlorine atom at the eight corners of the cube.

Thus there is 1/8 x 8 = 1atom of Cl and 1 atom of Cs.

Thus mass of unit cell of caesium chloride = 22.09 x 10^-23 g + 5.894 x 10^-23 g

Thus mass of unit cell of caesium chloride = 27.98 x 10^-23 g

Density of caesium chloride = mass of unit cell/volume of unit cell

Density of caesium chloride = 27.98 x 10^-23 g /(4.121) ³ x 10^-24 cm³.

Density of caesium chloride = 3.997 g/cm³ = 4 g/cm³

Ans: Density of caesium chloride = 4 g/cm³

Example – 04:

A metal crystallizes as fcc structure and the unit cell has a length of edge 3.72 x 10^-8 cm. Calculate the density of the metal. Given the atomic mass of metal as 68.5 g mol^-1.

Given: The edge length of the unit cell = a = 3.72 x 10^-8 cm, atomic mass of copper = M = 68.5 g/mol, Avogadro’s number N = 6.022 x 10²³ mol^-1. Type of crystal structure = face centred cubic

To Find: Density of metal =?

Solution:

The number of atoms in the unit cell of a face centred cubic structure is n = 4

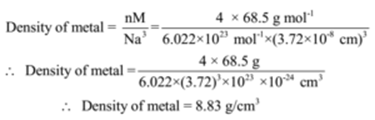
Ans: Density of metal = 8.83 g/cm³

Example – 05:

Sodium crystallizes in bcc structure. If the atomic radius of sodium is 186 pm. Find a) edge length b) volume of the unit cell and c) density of sodium crystal. The atomic mass of sodium is 23 g mol^-1.

Given: Atomic radius of sodium = r = 186 pm = 186 x 10^-10 cm = 1.86 x 10^-8 cm, atomic mass of copper = M = 23 g/mol, Avogadro’s number N = 6.022 x 10²³ mol^-1. Type of crystal structure = bcc

To Find: Edge length = a =? Volume of unit cell =? Density of sodium =?

Solution:

Volume of unit cell = a³ = (4.30 x 10^-8 cm) ³ = (4.3) ³ x 10^-24 cm³ = 79.4 x 10^-24 cm³

The density of sodium is 0.962 g cm^-3.

Ans: Density of sodium = 0.962 g/cm³

Example – 06:

copper crystallizes in fcc type unit cell. The edge length of a unit cell is 360.8 pm. The density of metallic copper is 8.92 g cm-3. Determine the atomic mass of copper.

Given: The edge length of the unit cell = a = 360.8 pm = 360.8 x 10^-10 cm  = 3.608 x 10^-8 cm, Density of copper  = 8.92 g cm^-3, Avogadro’s number N = 6.022 x 10²³ mol^-1. Type of crystal structure = fcc

To Find: the atomic mass of copper =?

Solution:

The number of atoms in the unit cell of a face centred cubic structure is n = 4

Ans: The atomic mass of copper is 63.07 g mol^-1.

Example – 07:

Silver crystallises in fcc type unit cell. The edge length of a unit cell is 4.07 10^-8 cm. The density of metallic silver is 10.5 g cm^-3. Determine atomic mass of silver.

Given: The edge length of the unit cell = a = 4.07 x 10^-8 cm, Density of silverr = 10.5 g cm^-3, Avogadro’s number N = 6.022 x 10²³ mol^-1. Type of crystal structure = fcc

To Find: Atomic mass of silver =?

Solution:

The number of atoms in the unit cell of a face centred cubic structure is n = 4

Ans: The atomic mass of silver is 106.6 g mol^-1

Example – 08:

Face centred cubic crystal lattice of copper has a density of 8.966 g cm^-3. Calculate the volume of the unit cell. Given the molar mass of copper 63.5 g/mol.

Given: Molar mass of copper = 63.5 g mol^-1, Density of copper = 8.966 g cm^-3, Avogadro’s number N = 6.022 x 10²³ mol^-1. Type of crystal structure = fcc

To Find: Volume of unit cell =?

Solution:

The number of atoms in the unit cell of a face centred cubic structure is n = 4

Ans: The volume of the unit cell is 4.704 x 10^-23 cm³

Example – 09:

Silver crystallizes as fcc structure. If the density of silver is 10.51 g cm^-3. Calculate the volume of a unit cell. Given:  molar mass of silver 108 g/mol.

Given: Molar mass of silver = 108 g mol^-1, Density of silver  = 10.51  g cm^-3, Avogadro’s number N = 6.022 x 10²³ mol^-1. Type of crystal structure = fcc

To Find: Volume of unit cell =?

Solution:

The number of atoms in the unit cell of a face centred cubic structure is n = 4

Ans: The volume of the unit cell is 6,825 x 10^-23 cm³

Science > Chemistry > Solid State > Numerical Problems on Density of Solid