Science > Chemistry > Chemical Thermodynamics and Energetics > Gibb’s Energy and Spontaneity
The Concept of Gibb’s Free Energy (G):
By the second law of thermodynamics, STotal = ΔSSystm + ΔSSurroundings
Thus to decide spontaneity of the process we have to determine the change in entropy of the system and the change in entropy of the surroundings. In chemistry, we are not concerned about the change in entropy of the surroundings. Hence to overcome this problem J. W. Gibbs introduces another thermodynamic property called Gibbs energy without considering the change in entropy of the surroundings.
Gibbs energy is defined as G = H – TS
Where H = Enthalpy of a system, T = Temperature of the system, S = Entropy of a system
H, T and S are state functions hence G is also a state function. Unit of G is J mol-1.
At constant temperature ΔG = ΔH – T ΔS
Derivation of Gibb’s Helmholtz Equation:
Gibbs energy is defined as G = H – TS …………..(1)
But H = U = PV ……………(2)
Where, H = Enthalpy of the system, T = Temperature of the system, S = Entropy of the system
U = Internal energy of the system, P = Pressure of the system, V = Volume of the system
From equations (1) and (2) we get
G = U + PV – TS
The change in Gibb’s energy in the process is given by
ΔG = ΔU + Δ(PV) – Δ(TS)
At constant pressure and temperature
ΔG = ΔU + PΔV – TΔS ….(3)
But at constant pressure
ΔU + PΔV = ΔH
Substituting in equation (3) we get
ΔG = ΔH – TΔS
This equation is known as Gibb’s Helmholtz Equation.
Gibb’s Energy and Spontaneity:
The total entropy changed in the process is given by
STotal = ΔSSystm + ΔSSurroundings
STotal = ΔS + ΔSSurroundings
ΔSTotal = ΔS + ΔSSurroundings ………………. (1)
Here, ΔS = ΔSSystm
If ΔH is enthalpy change which accompanies the process, then the enthalpy change in surroundings is – ΔH.
By definition of entropy,
Substituting in equation (1)

As T is always positive we can say that ΔG and ΔS have opposite signs. Thus in the non-spontaneous process, Gibbs’s energy increases while in spontaneous process Gibbs’s energy decreases. The spontaneity of reaction can be determined by following relations.
- If ΔG < 0, the process is spontaneous
- If ΔG > 0, the process is non-spontaneous
- If ΔG = 0, the process is in equilibriums
Example – 1:
Determine whether the reaction with ΔH = – 40 kJ and ΔS = +135 J K-1 at 300 K is spontaneous or not. Also, predict the nature exothermic or endothermic.
Solution:
Given: ΔH = – 40 kJ and ΔS = +135 J K-1 = + 0.135 kJ K-1, T = 300 K.
To Find: Nature of reaction
Gibb’s energy is given by ΔG = ΔH – TΔS
∴ ΔG = – 40 kJ – 300 K × 0.135 kJ K-1 = – 40 kJ – 40.5 kJ = -80.5 kJ
ΔG is negative i.e. ΔG < 0, the process is spontaneous
ΔH is negative i.e. ΔH < 0, the process is exothermic.
Example – 2:
Determine whether the reaction with ΔH = – 60 kJ and ΔS = – 160 J K-1 at 400 K is spontaneous or not. Also, predict the nature exothermic or endothermic.
Solution:
Given: ΔH = – 60 kJ and ΔS = – 160 J K-1 = – 0.160 kJ K-1, T = 400 K.
To Find: Nature of reaction
Gibb’s energy is given by ΔG = ΔH – TΔS
∴ ΔG = – 60 kJ – 400 K × (-0.160 kJ K-1) = – 60 kJ + 64 kJ = + 4 kJ
ΔG is positive i.e. ΔG > 0, the process is non-spontaneous
ΔH is negative i.e. ΔH < 0, the process is exothermic.
Example – 3:
Determine whether the reaction with ΔH = – 110 kJ and ΔS = + 40 J K-1 at 400 K is spontaneous or not. Also, predict the nature exothermic or endothermic.
Solution:
Given: ΔH = – 110 kJ and ΔS = +40 J K-1 = + 0.040 kJ K-1, T = 400 K.
To Find: Nature of reaction
Gibb’s energy is given by ΔG = ΔH – TΔS
∴ ΔG = – 110 kJ – 400 K × 0.040 kJ K-1 = – 110 kJ – 16 kJ = – 126 kJ
ΔG is negative i.e. ΔG < 0, the process is spontaneous
ΔH is negative i.e. ΔH < 0, the process is exothermic.
Example – 4:
Determine whether the reaction with ΔH = + 50 kJ and ΔS = -130 J K-1 at 250 K is spontaneous or not. Also, predict the nature exothermic or endothermic.
Solution:
Given: ΔH =+ 50 kJ and ΔS = – 130 J K-1 = – 0.130 kJ K-1, T = 250 K.
To Find: Nature of reaction
Gibb’s energy is given by ΔG = ΔH – TΔS
∴ ΔG = + 50 kJ – 250 K × ( -0.130 kJ K-1) = + 50 kJ + 32.5 kJ = + 82.5 kJ
ΔG is positive i.e. ΔG > 0, the process is non-spontaneous
ΔH is positive i.e. ΔH > 0, the process is endothermic.
Temperature of Equilibrium:
At equilibrium, the process is neither spontaneous nor non-spontaneous and ΔG = 0.
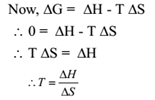
This is the temperature at which change over between spontaneous and non-spontaneous behaviour occurs.
Example – 5:
For a certain reaction, ΔH = – 25 kJ and ΔS = -40 J K-1 at what temperature will it change from spontaneous to non-spontaneous.
Given: ΔH = – 25 kJ and ΔS = – 40 J K-1 = – 0.040 kJ K-1,
To Find: T =?
We have T = ΔH / ΔS
T = – 25 / – 0.040 = 625 K
Ans: At a temperature of 625 K the reaction change from spontaneous to nonspontaneous.
Example – 6:
For a certain reaction, ΔH = – 224 kJ and ΔS = – 153 J K-1 at what temperature will it change from spontaneous to non-spontaneous.
Given: ΔH = – 224 kJ and ΔS = – 153 J K-1 = – 0.153 kJ K-1,
To Find: T =?
We have T = ΔH / ΔS
T = – 224 / – 0.153 = 1464 K
Ans: At a temperature of 1464 K the reaction change from spontaneous to nonspontaneous.
Example – 7:
Determine ΔSTotal for the reaction and discuss its spontaneity at 298 K.
Fe2O3(s) + 3CO(g) → 2Fe(s) + 3 CO2(g), ΔH° = -24.8 kJ, ΔS° = 15 J K-1.
Given: ΔH° = – 24.8 kJ, ΔS° = 15 J K-1, T = 298 K
To Find: ΔSTotal = ?
We have ΔSSurr = – ΔH° / T
ΔSSurr = – ΔH° / T = – (-24.8 kJ)/ 298 K = + 0.0832 kJ K-1 = + 83.2 J K-1
Now ΔSSys = ΔS° = 15 J K-1.
Now, ΔSTotal = ΔSSurr + ΔSSys = + 83.2 J K-1 + 15 J K-1 = 98.2 15 J K-1 .
ΔSTotal is positive i.e. ΔSTotal > 0, hence reaction is spontaneous at 298 K
Ans: ΔSTotal = 98.2 15 J K-1, The reaction is spontaneous at 298 K
Example – 8:
Determine ΔSTotal for the reaction and discuss its spontaneity at 298 K.
HgS(s) + O2(g) → Hg(l) + SO2(g), ΔH° = -238.6 kJ, ΔS° = + 36.7 J K-1.
Given: ΔH° = -238.6 kJ, ΔS° = + 36.7 J K–, T = 298 K
To Find: ΔSTotal = ?
We have ΔSSurr = – ΔH° / T
ΔSSurr = – ΔH° / T = – (- 238.6 kJ)/ 298 K = + 0.8006 kJ K-1 = + 800.6 J K-1
Now ΔSSys = ΔS° = + 36.7 J K-1.
Now, ΔSTotal = ΔSSurr + ΔSSys = + 800.6 J K-1 + 36.7 J K-1 = + 837.3 J K-1 .
ΔSTotal is positive i.e. ΔSTotal > 0, hence reaction is spontaneous at 298 K
Ans: ΔSTotal = + 837.3 J K-1, The reaction is spontaneous at 298 K.
ΔG and Equilibrium Constant:
The change in Gibb’s energy of reaction, related to standard Gibb’s energy is given by
ΔG = ΔG° + RT ln Q
At equilibrium ΔG = 0 and Q = K, thus equation becomes
ΔG° = – RT ln K
∴ ΔG° = – 2.303 RT log10K
This equation gives the relation between standard Gibb’s energy of the reaction and its equilibrium constant.
Relation Between ΔG and Non Mechanical Work:
According to First law of Thermodynamics
DU = q + W
Here W includes two types of work pressure-volume work (Mechanical) and non-expansive work (non mechanical).
ΔU = q – PΔV + WNon-Exp
∴ q = ΔU + PΔV – WNon-Exp
∴ q = ΔH – WNon-Exp ………. (1)
For isothermal and reversible condition we have

Thus Gibb’s energy gives us the measure of non-expansion work done by the system.
Third Law of Thermodynamics:
It states that the entropy of a perfectly ordered crystalline substance is zero at absolute zero of temperature. Thus S = 0 at T = 0 for perfectly crystalline substance.
If crystal contains some impurity or some disorder in its structure its entropy is always greater than zero at T = 0. Such entropy of the substance is called residual entropy of the system. The third law helps in determination of absolute entropy of any substance either solid, liquid or in the gaseous state.
The significance of Third Law of Thermodynamics:
- It gives absolute datum from which entropy can be measured.
- Using this law absolute entropy of any substance either solid, liquid or in the gaseous state at a temperature above 0 K can be obtained.
- Standard entropy change ΔS° for a reaction can be calculated and hence the spontaneity of reaction can be determined.
- The standard enthalpy S of a pure substance can be measured at 25 °C and 1 atm pressure.
Note:
For perfectly crystalline substance absolute entropy is zero (S0 = 0) at absolute zero (0 K)
As the temperature increases say to T K its absolute entropy changes to ST.
Change in entropy is given by ΔS = ST – S0
i.e. ΔS = ST – 0 = ST.
This shows that it impossible for any substance to have an absolute entropy zero at temperature greater than 0 K
Entropy Change Due to Increase in Temperature:
The increase in entropy is given by
ΔS = ST – S0
Where, ST = Absolute entropy of substance at temperature T
S0 = Absolute entropy of substance at temperature 0 K = 0
ΔS = ST – S0 = ST – 0= ST
ST can be determined by the relation

Where CP = Molar heat capacity at constant pressure.
Standard Molar Entropy:
We know that entropy is the measure of disorderedness. Disorder of any substance depends on the mass of the substance, its molecular and its condition of temperature and pressure.
The absolute entropy(S) of 1 mole of pure substance at 1 atm pressure and 25 °C is called the standard molar entropy of the substance.By knowing the values of standard molar entropy of all reactants and products in chemical reaction we can calculate ΔS° of the reaction using the relation
ΔS° = ∑ ΔS°Products – ∑ ΔS°Reactants
The standard molar entropy is useful in comparison of entropies of different substances under the same conditions of temperature and pressure.
Previous Topic: The Concept of Entropy of a System
For More Topics in Chemistry Click Here