Hess’s Law and its Applications

Science > Chemistry > Chemical Thermodynamics and Energetics > Hess’s Law and its Applications

In this article, we shall study Hess’s law and its applications in thermochemistry.

Statement :

It states that the change in enthalpy accompanying a chemical reaction is independent of the pathway between initial and final states of the chemical reaction.

Explanation:

Let us suppose substance ‘A’ is converted into D directly.

A   →   D,                ΔH =   Q kJ

Suppose the same change is brought about in different steps,

i) A   →  B,               ΔH₁     =   Q₁ kJ

ii)  B → C,                ΔH₂    =   Q₂ kJ

iii)  C →D ,                ΔH₃   =   Q₃ kJ

Representation:

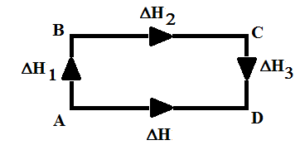
Then, according to Hess’s law,

ΔH = ΔH₁ + ΔH₂ + ΔH₃

Q   =   Q₁   +   Q₂   + Q₃

Thus, Hess’s law implies that change in enthalpy of a chemical reaction depends upon the initial and final state of a chemical reaction irrespective of the number of steps involved in a chemical reaction.

Illustration:

The change in enthalpy of formation of carbon dioxide can be determined in two ways.

One-step preparation:

Solid carbon is burnt in excess of oxygen.

C_(s) + O_2(g)  →  CO_2(g)   , Δ H  =  -395.39 kJ

Preparation in two steps:

Step – 1: Solid carbon is burnt in limited supply of oxygen to form carbon monoxide,

C_(s) + 1/2O_2(g)  →  CO_(g)   , Δ H₁ = -111.7 kJ

Step – 2: Carbon monoxide is then burnt in excess of oxygen to from carbon dioxide,

CO_(g)+ 1/2O_2(g)  → CO_2(g , ΔH₂=  -283.67 kJ

According to Hess’s law,

Δ H₁ + ΔH₂ =   -111.7 kJ  –  283.67 kJ  = -395.39 kJ   = ΔH

Thus Hess’s law is illustrated.

Applications of Hess’s Law:

• Thermochemical equations can be added subtracted or multiplied like ordinary algebraic equations.
• Hess’s law is useful to calculate heats of many reactions which do not take place directly.
• It is useful to find out heats of extremely slow reaction.
• It is useful to find out the heat of formation, neutralization, etc.

Numerical Problems Based on Hess’s Law:

Example – 01:

Calculate the enthalpy of formation of CO from given data

i) C_(s) + O_2(g)  →   CO_2(g)              ΔH° = -393.5 KJ 

ii) CO_(g)+ ½O_2(g)  →   CO_2(g)      ΔH° = – 283.0 KJ 

Solution:

The formation of carbon monoxide is represented by following thermochemical equation

C_(s) + ½O_2(g)  →   CO_(g)      ΔH° = ?

Keeping given equation (i) as it is and reversing equation (ii) we get

i) C_(s) + O_2(g)  →   CO_2(g)              ΔH₁° = -393.5 KJ 

iii) CO_2(g)  →    CO_(g)+ ½O_2(g)    ΔH₂° = + 283.0 KJ 

Adding equations (i) and (iii) and by Hess’s Law we get

C_(s) + ½O_2(g)  →   CO_(g)      ΔH° = ΔH₁° +  ΔH₂° =  -393.5 KJ + 283.0 KJ

C_(s) + ½O_2(g)  →   CO_(g)      ΔH° =  -110.5 KJ

Ans: Hence enthalpy of formation of CO is – 110.5 kJ mol^-1

Example – 02:

Calculate the enthalpy of formation of CH₄ from given data

i) C_(s) + O_2(g)  →   CO_2(g)                                   ΔH° = -393.5 KJ 

ii) H_2(g) + ½O_2(g)  →   H₂O_(l)                           ΔH° = – 285.8 KJ 

iii) CH_4(g) + 2O_2(g)  →   CO_2(g)  +  2 H₂O_(l)    ΔH° = – 890.3 KJ 

Solution:

The formation of CH₄ is represented by following thermochemical equation

C_(s) + 2H_2(g)  →   CH_4(g)      ΔH° = ?

Keeping given equation (i) as it is, multiplying equation (ii) by 2 and reversing equation (ii) we get

i) C_(s) + O_2(g)  →   CO_2(g)                                      ΔH₁° = -393.5 KJ 

iv) 2 H_2(g) +  O_2(g)  →   2 H₂O_(l)                           ΔH₂° = – 571.6 KJ 

v)   CO_2(g)  +  2 H₂O_(l)   →  CH_4(g)+ 2O_2(g)     ΔH₃° = + 890.3 KJ 

Adding equations (i) (iv) and (v) and by Hess’s Law we get

C_(s) + 2H_2(g)  →   CH_4(g)    ΔH° = ΔH₁° +  ΔH₂° +  ΔH₃° = -393.5 KJ – 571.6 KJ  + 890.3 kJ

C_(s) + 2H_2(g)  →   CH_4(g)     ΔH° =  – 74.8 KJ

Ans: Hence enthalpy of formation of CH₄ is – 74.8 kJ mol^-1

Example – 03:

Calculate the ΔH° for the reaction

2 ClF_(g) + O_2(g)  →   Cl₂O_(g)    + OF_2(g)

From following equations

i) F_2(g)  +   ClF_(g)  →   ClF_3(l)                                       ΔH° = – 139.2 KJ 

ii) 2 ClF_3(l)  + 2 O_2(g)  →   Cl₂O_(g)  + 3 OF_2(g)         ΔH° = + 533.4 KJ 

iii) F_2(g) +½O_2(g)  →   OF_2(g)                                      ΔH° = + 24. 7 KJ 

Solution:

Required reaction is

2 ClF_(g)+ O_2(g)  →   Cl₂O_(g)    + OF_2(g)

Multiplying equation (i) by 2, keeping equation (ii) as it is, and multiplying equation (iii) by 2 and reversing it.

iv) 2 F_2(g)  +   2 ClF_(g)  →   2 ClF_3(l)                            ΔH° = – 278.4 KJ 

ii) 2 ClF_3(l)  + 2 O_2(g)  →   Cl₂O_(g)  + 3 OF_2(g)         ΔH° = + 533.4 KJ 

v) 2 OF_2(g)     →   2 F_2(g)+    O_2(g)                              ΔH° = – 49.4  KJ 

Adding equations (iv) (ii) and (v) and by Hess’s Law we get

2 ClF_(g)+ O_2(g)  →   Cl₂O_(g)    + OF_2(g)   ΔH° = ΔH₁° +  ΔH₂° +  ΔH₃° = – 278.4 KJ  + 533.4 KJ  – 49.4 kJ

2 ClF_(g) + O_2(g)  →   Cl₂O_(g)    + OF_2(g)   ΔH° = + 205.6 KJ

Hence ΔH° for the reaction is 205.6 kJ

Example – 04:

Calculate the ΔH° for the reaction between ethene with water to form ethanol from the following data.

From following equations

i) C₂H₅OH_(l)  +   3 O_2(g)  →   2CO_2(g)  + 3 H₂O_(l)     ΔH° = – 1368 KJ 

ii) C₂H_4(g)  +   3 O_2(g)  →   2CO_2(g)  + 2 H₂O_(l)          ΔH° = – 1410 KJ 

Is  ΔH° calculated the enthalpy of formation of liquid ethanol?

Solution:

The reaction between ethene and water is represented by

C₂H_4(g)  +   H₂O_(l)   →   C₂H₅OH_(l)         ΔH° = ?

Reversing equation (i), keeping equation (ii) as it is

iii) 2CO_2(g)  + 3 H₂O_(l)  → C₂H₅OH_(l)  +   3 O_2(g)    ΔH° = + 1368 KJ 

ii) C₂H_4(g)  +   3 O_2(g)  →   2CO_2(g)  + 2 H₂O_(l)          ΔH° = – 1410 KJ

Adding equations (iii) and (ii) and by Hess’s Law we get

C₂H_4(g)  +   H₂O_(l)   →   C₂H₅OH_(l)         ΔH° = ΔH₁° +  ΔH₂° = 1368 KJ  -1410 KJ 

C₂H_4(g)  +   H₂O_(l)   →   C₂H₅OH_(l)         ΔH° = – 42 kJ

Hence ΔH° for the reaction is – 42 kJ

This cannot be the heat of formation of ethanol, because it is not obtained from its constituent elements in their standard state.

Example – 05:

Calculate the ΔH° for the reaction       2C_(graphite)  +   3 H_2(g)  →   C₂H_6(g)  

From following equations

i) C₂H_6(g)  +   7/2 O_2(g)  →   2CO_2(g)  +3 H₂O_(l)          ΔH° = – 1560 KJ 

ii)  H_2(g)  +  1/2 O_2(g)  →   H₂O_(l)                                   ΔH° = – 285.8 KJ 

ii)  C_(graphite)  +  O_2(g)  →   CO_2(g)                                  ΔH° = – 393.5 KJ 

Solution:

The required reaction is

2C_(graphite)  +   3 H_2(g)  →   C₂H_6(g)          ΔH° =?

Reversing equation (i), multiplying equation (ii) by 3 and multiplying equation (iii) by 2 we get

iv) 2CO_2(g)  +3 H₂O_(l)   →   C₂H_6(g)  +   7/2 O_2(g)          ΔH° = + 1560 KJ 

v)  3H_2(g)  + 3/2 O_2(g)  →   3 H₂O_(l)                                   ΔH° = – 857.4 KJ 

vi)  2C_(graphite)  +  2O_2(g)  →   2CO_2(g)                               ΔH° = – 787.0 KJ 

Adding equations (iv), (v) and (vi) and by Hess’s Law we get

2C_(graphite)  +   3 H_2(g)  →   C₂H_6(g) , ΔH° = ΔH₁° +  ΔH₂° +  ΔH₃° = 1560 KJ  -857.4 KJ  – 787 kJ

2C_(graphite)  +   3 H_2(g)  →   C₂H_6(g)  ΔH° = – 84.4 kJ

Ans: Hence ΔH° for the reaction is – 84.4 kJ

Example – 06:

Calculate the standard enthalpy for the reaction      

2Fe_(s) +   3/2 O_2(g)  →  Fe₂O_3(s)  

From following equations

i) 2 Al_(s)  +  Fe₂O_3(s)    →   2Fe_(s)  + Al₂O_3(s)         ΔH° = – 847.6 KJ 

ii) 2 Al_(s)    +  3 /2 O_2(g)  →   Al₂O_3(s)                       ΔH° = – 1670 KJ 

Solution:

The required reaction is

2Fe_(s)  +   3/2 O_2(g)  →  Fe₂O_3(s)           ΔH° =?

Reversing equation (i), keeping equation (ii) as it is we get

iii) 2Fe_(s)  + Al₂O_3(s)    →  2 Al_(s)  +  Fe₂O_3(s)          ΔH° =  847.6 KJ 

ii) 2 Al_(s)    +  3 /2 O_2(g)  →   Al₂O_3(s)                       ΔH° = – 1670 KJ 

Adding equations (iii) and (ii) we get

2Fe_(s)  +   3/2 O_2(g)  →  Fe₂O_3(s)      ΔH° = ΔH₁° +  ΔH₂° = 847.6 KJ  – 1670 KJ

2Fe_(s)  +   3/2 O_2(g)  →  Fe₂O_3(s) ,   ΔH° = – 822.4 kJ

Hence standard enthalpy of the reaction is – 822.4 kJ

Example – 07:

Given the following equations and ΔH° at 25 °C     

i)  Si_(s)  + O_2(g)     →    SiO_2(s)                  ΔH° = – 911 KJ 

ii) 2C_(graphite)  +  O_2(g)  →   2CO_(g)         ΔH° = – 221 KJ 

iii)   Si_(s)    +  C_(graphite)   →   SiC_(s)           ΔH° = – 65.3 KJ 

Calculate ΔH° for the reaction SiO_2(s)    + 3 C_(graphite)   →   SiC_(s)    +    2CO_(g) 

Solution:

The required reaction is

SiO_2(s)    + 3 C_(graphite)   →   SiC_(s)    +    2CO_(g)         ΔH° =?

Reversing equation (i), keeping equations (ii) and (iii)  as it is we get

iv)  SiO_2(s)       →    Si_(s)  + O_2(g)           ΔH° =  911 KJ 

ii) 2C_(graphite)  +  O_2(g)  →   2CO_(g)         ΔH° = – 221 KJ 

iii)   Si_(s)    +  C_(graphite)   →   SiC_(s)           ΔH° = – 65.3 KJ 

Adding equations (iv), (ii) and (iii) and by Hess’s Law we get

SiO_2(s)    + 3 C_(graphite)   →   SiC_(s)    +    2CO_(g)         ΔH°  = ΔH₁° +  ΔH₂° +  ΔH₃° = 911 kJ  -221 kJ -65.3 kJ

SiO_2(s)    + 3 C_(graphite)   →   SiC_(s)    +    2CO_(g)         ΔH°  = + 624.7 kJ

Hence ΔH°   for the reaction is 624.7 kJ

Example – 08:

Given the following equations and ΔH° at 25 °C     

i)  2H₃BO_3(aq)     →    B₂O_3(s)    +   3 H₂O_(l) ΔH° = + 14.4 KJ 

ii) H₃BO_3(aq)    →   HBO_2(aq)    +  H₂O_(l)            ΔH° = – 0.02 KJ 

iii)   H₂B₄O_7(s)     →   2 B₂O_3(s)    +  H₂O_(l) ΔH° = 17.3  KJ 

Calculate ΔH° for the reaction H₂B₄O_7(s)   + H₂O_(l)    →   4 HBO_2(aq)

Solution:

The required reaction is

H₂B₄O_7(s)   + H₂O_(l)    →   4 HBO_2(aq)       ΔH° =?

Reversing equation (i) and multiplying by 2, Multiplying equations (i) by4 keeping equation (iii)  as it is we get

iv)  2B₂O_3(s)    +   6 H₂O_(l)    →    4 H₃BO_3(aq)   ΔH° = – 28.8 KJ 

v) 4  H₃BO_3(aq)    →   4 HBO_2(aq)    +  4 H₂O_(l)        ΔH° = – 0.08 KJ 

iii)   H₂B₄O_7(s)     →   2 B₂O_3(s)    +  H₂O_(l) ΔH° = 17.3  KJ

Adding equations (iv), (v) and (iii) and by Hess’s Law we get

H₂B₄O_7(s)   + H₂O_(l)    →   4 HBO_2(aq)       ΔH° = ΔH₁° +  ΔH₂° +  ΔH₃° = – 28.8 kJ  – 0.08 kJ + 17.3kJ

H₂B₄O_7(s)   + H₂O_(l)    →   4 HBO_2(aq)       ΔH° = – 11.58 kJ

Hence ΔH°   for the reaction is -11.58 kJ

Previous Topic: Concept of Bond Enthalpy

Next Topic: Concept of Entropy of a System

Science > Chemistry > Chemical Thermodynamics and Energetics > Hess’s Law and its Applications