First Order Reaction

Science > Chemistry > Chemical Kinetics > Rate of First Order Reaction

In this article, we shall study the order of reaction and the analytical treatment to the first-order reaction, and the rate of the first-order reaction.

Order of Reaction:

The overall order of the reaction is defined as the sum of the exponents to which the concentration terms in the rate law are raised.

Let us consider a general reaction

aA  + bB  → Products

The rate law can be written as

Rate = K  [A]^x [B]^y …………… (1)

Thus the overall order of reaction is (x + y).

Example:

In the reaction, 

NO_2(g)   +   CO_(g)  →  NO_(g)   + CO_2(g)

The rate of reaction is experimentally found to proportional

to [NO₂]² and independent of [CO]. Thus x = 2 and y = 0

Thus the rate law of reaction is

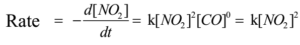
Thus the overall order of the reaction is 2.

Characteristics of Order of Reaction:

• Order of reaction represents the number of atoms, ions and molecules whose concentration influence the rate of reaction.
• Order of the reaction is defined as the sum of the exponents to which the concentration terms in the rate law are raised. Thus it is not dependent on the stoichiometric coefficients in a balanced chemical reaction.
• Values of x and y are determined experimentally. The values of x and y in the rate law are not necessarily equal to the stoichiometric coefficients of reactants. Thus the order of reaction can be decided by performing experiment only.
• Order of reaction is defined in terms of concentration of reactants only and not of products.
• Order of reaction may be integer, fraction or zero.

Reactions with No Order:

If the rate of reaction cannot be expressed in the form, Rate, then the reaction has no order and term order should not be used for such reactions.

Example:

Clear Concept of Stoichiometric Coefficients of Balanced Chemical Equations and Exponents in Rate Law:

Let us consider a general reaction

aA  + bB  → Products

The stoichiometric coefficients of A and B are a and b.

Let us assume that the rate of reaction depends on [A]^x and [B]^y

The rate law is written as

Rate = K  [A]^x [B]^y …………… (1)

The values of x and y for the reaction are found experimentally. The values of x and y may be integer, fraction or zero.

First Order Reactions:

Integrated Rate Law For First Order Reaction:

The equations which are obtained by integrating the differential rate laws and which gives the direct relationship between the concentrations of the reactants and time is called integrated rate laws. A reaction whose rate depends on the single reactant concentration is called the first-order reaction.

Let us consider a general reaction

Let [A]_o be initial concentration of A (i.e at t = 0)  and [A]_t be the final concentration of A (i.e at t = t)

Integrating both sides of above equation

This relation is known as exponential integrated law for first order reaction.

The Expression for the Integrated Rate Constant for First Order Reaction:

This is an expression for the integrated rate constant for the first order reaction.

The expression for the integrated rate constant in terms of initial concentration for First Order Reaction:

Let a mol dm^-3 be the initial concentration of A (i.e at t = 0) and at some instant ‘t’ the decrease in concentration is x mol dm^-3.  (i.e at t = t). Thus   [A]_o = a and  [A] = a – x

Substituting in equation (2) we have

This is an expression for the integrated rate constant for the first order reaction in terms of initial concentration.

Unit of  the Integrated Rate Constant for the First Order Reaction:

The integrated rate constant for the first order reaction is given by

The quantity [A]_o / [A]  is a pure ratio. Hence it has no unit. Thus the unit of  integrated rate constant is per unit time (s^-1 or  min^-1 , hr^-1 )

Half-Life of First Order Reaction:

The half-life of a reaction is defined as the time required for the reactant concentration to fall to one half of its initial value. Thus for t = t1/2,  [A] = ½ [A]_o

The  integrated rate constant for the first order reaction is given by

This is an expression for the half-life of the first-order reaction.

Graphical Representation of Half-Life:

A graph is drawn by plotting time as a multiple of half-life on the x-axis and the concentration of reactant in terms of original concentration on the y-axis at that instant. The graph is as follows.

The graph shows that it is an exponential process. Thus this process will never complete. i.e. the graph will never touch x-axis.

Note: Such graph is shown by the disintegration of a radioactive element. The radioactive elements obey decay law.

Graphical Representation of the First Order Reaction in Different Ways:

The graph of Rate of reaction against time:     

The differential rate law for the first order reaction is

It is of the form y = mx + c. Thus the graph of rate reaction versus concentration at an instant  is a straight line passing through the origin (since c = 0). The slope of the straight line is k.

The graph of Concentration of the reactants of against time:

The exponential rate law for the first order reaction is [A]_t = [A]_o e^-kt

Thus it is an exponential process. Thus this process will never complete. i.e. the graph will never touch x-axis.

The graph of Concentration of the reactants against time:

This equation is of form y = mx + c. Thus the graph of  log₁₀[A]_t  versus time is a straight line with y-intercept log₁₀[A]₀.

The graph of log₁₀([A]₀/ [A]_t) against time:

This equation is of form y = mx + c. Where c = 0. Thus the graph of  log₁₀([A]₀/ [A]_t) versus time is  a straight line passing through the origin

Examples of First-order Reactions:

Pseudo First Order Reaction:

The reactions that have higher order true rate law are found to behave as the first order are called pseudo-first order reactions.

Examples of Pseudo First Order Reactions:

• Hydrolysis of methyl acetate:

CH₃COOCH_3(aq)  + H₂O_(l) → CH₃COOH_(aq)) + CH₃OH_(aq)

The true rate law of reaction must be

Rate = K'[CH₃COOCH₃][H₂O]

Thus it seems that the rate of reaction is dependent on two reactants.

But the concentration [H₂O]  is constant (say k’’)

Rate = K’ K”[CH₃COOCH₃]

Hence,  Rate = K[CH₃COOCH₃]

Thus the reaction actually a first order reaction. Hence it is called as pseudo first order reaction.

• Hydrolysis of cane sugar (sucrose):

Science > Chemistry > Chemical Kinetics > Rate of First Order Reaction