Probability: Normal Distribution

Science > Mathematics > Statistics and Probability > Probability > Normal Distribution 01

The normal distribution refers to a family of continuous probability distributions described by the normal equation.

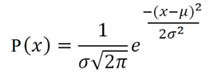
on the domain x ∈ (- ∞, ∞)

where x is a normal random variable, μ is the mean, σ is the standard deviation,

Thus the normal distribution can be completely specified by two parameter mean (μ) and standard deviation (σ) and is represented as N(μ, σ).

Mathematicians called this distribution a normal distribution, a physicist called it a Gaussian distribution, and scientists called it a bell curve due to its bell-like shape.

The normal distribution with mean μ = 0 and standard deviation, σ = 1 is called the standard normal distribution. It is denoted by N(0, 1).

Characteristics of a Normal Distribution

• The normal curve is symmetrical about the mean μ. It is perfectly symmetrical around its center. That is, the right side of the center is a mirror image of the left side.
• The mean is at the middle and divides the area into halves. The center of a normal distribution is located at its peak, and 50% of the data lies above the mean, while 50% lies below. It means that the mean, median, and mode are all equal in a normal distribution.
• There is also only one mode, or peak, in a normal distribution.
• Normal distributions are continuous and have tails that are asymptotic.
• The total area under the curve is equal to 1;
• It is completely determined by its mean and standard deviation (SD) σ (or variance σ²)
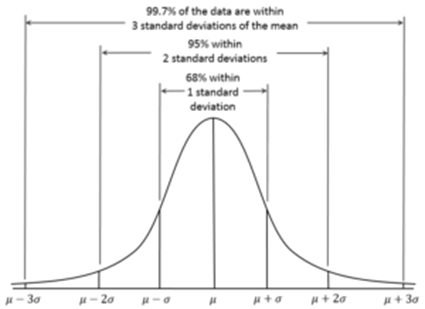
• Approximately 68 % of the data lies within 1 SD of the mean. Approximately 95 % of the data lies within 2 SD of the mean.  Approximately 99.7 % of the data lies within 3 SD of the mean.

The Z – score:

The number of standard deviations from the mean is called the standard score or z – score.

An arbitrary normal distribution can be converted to a standard normal distribution by changing variables to z.

Empirical Rules for z – Scores:

• Approximately 68 % of the data lies within 1 SD of the mean. 
• Approximately 95 % of the data lies within 2 SD of the mean. 
• Approximately 99.7 % of the data lies within 3 SD of the mean.

Importance of z – Score:

Z-Scores tell us whether a particular score is equal to the mean, below the mean or above the mean of a bunch of scores. They can also tell us how far a particular score is away from the mean.

Z-Score	Conclusion
0	It is equal to the group mean
Positive	It is above the group mean
Negative	It is below the group mean
+ 1	It is 1 Standard Deviation above the mean
+ 2	It is 2 Standard Deviation above the mean
– 1	It is 1 Standard Deviation below the mean
– 2	It is 1 Standard Deviation below the mean

We can use Z-scores to standardize scores from different groups of data. Then we can compare raw scores from different groups of data.

Example – 01:

95 % of students at the college are between 1.1 m and 1.7 m tall. Find mean and the standard deviation assuming a normal distribution.

Solution:

Mean = μ = average of the two values given = (1.1 + 1.7)/2 = 2.8/2 = 1.4 m

From empirical rule states that approximately 95 % of the data lies within 2 SD of the mean on either side.

Therefore the total deviation is 4 S.D.

4 S.D. = 1.7 – 1.1

4 S.D. = 0.6

1 S.D. = σ = 0.15 m

Ans: Mean = 1.4 m and the standard deviation is 0.15 m

Example – 02:

95 % of students in a class of 100 weigh between 62 kg and 90 kg. Find mean and standard deviation assuming a normal distribution.

Solution:

Mean = μ = average of the two values given = (62 + 90)/2 = 152/2 = 76 kg

From empirical rule states that approximately 95 % of the data lies within 2 SD of the mean on either side.

Therefore the total deviation is 4 S.D.

4 S.D. = 90 – 62

4 S.D. = 28

1 S.D. = σ = 7 kg

Ans: Mean = 76 kg and standard deviation is 7 kg

Example – 03:

68 % of marks of students in a certain test are between 51 and 64. Find mean and standard deviation assuming a normal distribution.

Solution:

Mean = μ = average of the two values given = (51 + 64)/2 = 115/2 = 57.5 kg

From empirical rule states that approximately 68 % of the data lies within 1 SD of the mean on either side.

Therefore the total deviation is 2 S.D.

2 S.D. = 64 – 51

2 S.D. = 13

1 S.D. = σ = 6.5 kg

Ans: Mean marks = 57.5 and standard deviation in marks is 6.5

Example – 04:

99.7 % of electrical components produced by a machine have lengths between 1.176 cm and 1.224 cm. Find mean and standard deviation assuming a normal distribution.

Solution:

Mean = μ = average of the two values given = (1.176 + 1.224)/2 = 2.4/2 = 1. 2 cm

From empirical rule states that approximately 99.7 % of the data lies within 3 SD of the mean on either side.

Therefore the total deviation is 6 S.D.

6 S.D. = 1.224 – 1.176

6 S.D. = 0.048

1 S.D. = σ = 0.008 cm

Ans: Mean length = 1.2 cm and standard deviation in length is 0.008 cm

For More Topics in Probability Click Here

For More Topics in Mathematics Click Here