Science > Physics > Rotational Motion > Angular Momentum
In this article, we shall study important physical quantity related to the rotational motion called the angular momentum.
The angular momentum of a rigid body about a given axis is defined as the product of its moment of inertia about the given axis and its angular velocity. It is denoted by letter ‘L’. Its S.I. unit is kg m² s-1 and its dimensions are [M1L2T-1]
Relation Between Angular Momentum and Angular Velocity of a Rigid Rotating Body:
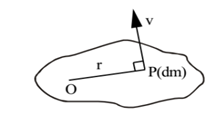
Consider a rigid body rotating about an axis passing through point O and perpendicular to the plane of the paper in an anticlockwise sense as shown. Consider infinitesimal element at P of mass dm in the plane of the paper. Let the distance of point P from the axis of rotation be r.
The moment of inertia of the rigid body is given by
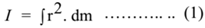
Let ‘v’ be the linear velocity of the element, then the magnitude of the linear momentum of the element is given by
dP = v .dm
Then, quantity dL = r . dp, is the magnitude of the angular momentum of the element. Similarly, we can find the angular moment of each and every element in the body. As all elements are moving in the same direction, resultant angular momentum can be calculated by integrating the above expression.

This is an expression for the angular momentum of a rotating body.
In vector form,

Principle of Conservation of Angular Momentum:
Statement:
If the external torque acting on the body or the system is zero, then the total vector angular momentum of a body or of a system remains constant.
Explanation:
For a rigid body rotating about the given axis, torque is given by
τ = I α
Where τ = torque acting on the rotating body
I = Moment of Inertia of the body about the given axis of rotation
α = Angular acceleration

For rigid body moment of inertia about the given axis of rotation is always constant.

As external torque acting on the body or the system is zero, τ = 0

Therefore, there is no change in angular momentum.
∴ L = constant,
but L = Iω
∴ L = Iω = constant
I1ω1 = I2ω2 = I3ω3 = ……. = Inωn = constant
Above relation indicates that as the moment of inertia decreases angular velocity increases and vice-versa. This is known as the principle of conservation of angular momentum.
Moment of Inertia of body changes if the distribution of mass about the axis of rotation changes.
Examples of Conservation of Angular Momentum:
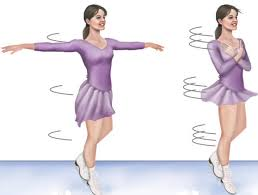
This principle is used by acrobats in the circus, ballet dancers, skaters etc. By extending or by pulling in the hands, legs, they change the distribution of mass about the axis of rotation and thus their angular velocity changes by keeping angular momentum constant. If they, extend their hands or legs the moment of Inertia increases thus angular velocity decreases. If they pull in their hands or legs the moment of inertia decreases thus angular velocity increases. When diver, want to execute somersault, he pulls in his arms and legs together, so that the moment of inertia decreases and his angular velocity increases.


Numerical Problems on Angular Momentum:
Example – 01:
If the earth had its radius suddenly decreased by half when spinning about its axis, what would the length of the day be?
Given: Radius of earth R2 = ½ R1, Present period = T1 = 24 hr
To Find: New period = T2 =?
Solution:
By the principle of conservation of angular momentum

Ans: New length of the day would be 6 hours
Example – 02:
What will be the duration of the day if the earth suddenly shrinks to 1/27 th of its original volume? The mass being unchanged.
Given: Volume of the earth V2 = 1/27 V1, Present period = T1 = 24 hr
To Find: New period = T2 =?
Solution:
By the principle of conservation of angular momentum


Ans: New duration of the day would be 2.67 hours
Example – 03:
A disc is rotating in a horizontal plane about a vertical axis at the rate of 5π/3 rad/s. A blob of wax of mass 0.02 kg falls vertically on the disc and adheres to it at a distance of 0.05 m from the axis of rotation. If the speed of rotation thereby becomes 40 rev/min, calculate the M. I. of the disc.
Given: Initial speed of rotation of disc = 5π/3 rad/s, Mass of blob = M = 0.02 kg, Distance from axis of rotation = r = 0.05 m, New angular speed = N = 40 rev/min
To Find: M.I. of disc = Id =?
Solution:
The angular speed after coupling is

Let M.I. of the disc be Id and that of bob be Ib.
By the principle of conservation of angular momentum

Ans: M.I. of the disc is 2 x 10-4 kg m2
Example – 04:
A horizontal disc is freely rotating about a vertical axis passing through its centre at the rate of 100 r.p.m. A blob of wax of mass 20 g falls on the disc and sticks to it at a distance of 5 cm from the axis. If the M. I. of the disc about the given axis is 2 x 10-4 kg m2, find the new frequency of rotation of the disc.
Given: Initial speed of rotation of disc = Nd = 100 r.p.m., Mass of blob = M = 20 g = 0.02 kg, Distance from axis of rotation = r = 5 cm = 0.05 m, M.I. of disc = Id = 2 x 10-4 kg m2
To Find: New frequency of rotation = N =?
Solution:
Let M.I. of the disc be Id and that of bob be Ib.
By the principle of conservation of angular momentum

Ans: New angular speed = 50 r.p.m.
Example – 05:
A horizontal disc is freely rotating about a vertical axis passing through its centre at the rate of 180 r.p.m. A blob of wax of mass 1.9 g falls on the disc and sticks to it at a distance of 25 cm from the axis. If the speed of rotation now is 60 r.p.m. Calculate the moment of inertia of the disc.
Given: Initial speed of rotation of disc = 180 r.p.m., Mass of bob = M = 1.9 g = 0.0019 kg, Distance from axis of rotation = r = 25 cm = 0.25 m, New angular speed = N = 60 r.p.m.
To Find: M.I. of disc = Id =?
Solution:
Let M.I. of the disc be Id and that of bob be Ib.
By the principle of conservation of angular momentum

Ans: M.I. of the disc is 5.94 x 10-4 kg m2
Example – 06:
A ballet dancer spins about a vertical axis at 120 r.p.m. with her arms outstretched. With her arms folded, the M. I. about the axis of rotation decreases by 40%. Calculate the new rate of revolution.
Given: Initial angular speed = 120 r.p.m., M.I. decreases by 40 %, I2 = I1 – 40% I1 = 0.6 I1,
To Find: New angular speed = N2 =?
Solution:
By the principle of conservation of angular momentum

Ans: New rate of revolution is 200 r.p.m.
Example – 07:
A ballet dancer spins about a vertical axis at 90 r.p.m. with her arms outstretched. With her arms folded, the M. I. about the axis of rotation changes to 75%. Calculate the new rate of revolution.
Given: Initial angular speed = 90 r.p.m., M.I. decreases to 75 %, I2 = 0.75 I1,
To Find: New angular speed = N2 =?
Solution:
By the principle of conservation of angular momentum

Ans: New rate of revolution is 120 r.p.m.
Example – 08:
A man is standing on a rotating chair with his arms fully outstretched. The chair rotates with a speed of 81 r.p.m. On bringing arms close to his body, the radius of gyration is reduced by 10%. What is the increase in the speed of rotation? (neglect the friction)
Given: Initial angular speed = N1 = 81 r.p.m., radius of gyration reduces by 10%, K2 = K1 – 10% K1 = 0.90 K1,
To Find: increase in angular speed = N2 – N1 =?
Solution:
By the principle of conservation of angular momentum

Ans: The Increase in angular speed = 100 – 81 = 19 r.p.m.
Example – 09:
A man standing with outstretched arms on a frictionless rotating turntable has a mass 0.2 kg in each hand. The M. I. of the system in this position is 150 kg m2. He slowly folds his arms until the M. I. is reduced to 60 kg m2. The angular velocity of the system is now 5 rad/s. Find the initial angular velocity and the new K.E. of the system.
Given: Initial M.I. of system = I1 = 150 kg m2. Final M.I. of system = I2 = 60 kg m2. Final angular speed = ω2 = 5 rad/s
To Find: Initial angular speed w1 =? Final K.E. =?
Solution:
By the principle of conservation of angular momentum

Final K.E. = ½ I w2 = ½ x 60 x (5)2 = 750 J
Ans: Initial angular speed = 2 rad/s, Final kinetic energy = 750 J.
Example – 10:
A wheel is rotating with an angular speed of 500 r.p.m. on a shaft. A second identical wheel initially at rest is suddenly coupled to the same shaft. What is the angular speed of the combination? Assume that the M.I. of the shaft is negligible.
Given: Initial speed of rotation of first wheel = N1 = 500 r.p.m.,
To Find: New frequency of rotation = N =?
Solution:
M.I. of the first wheel = I1 and M.I. of the second wheel = I2,
Let N be their final common angular speed.
The two wheels are identical. I1 = I2.
By the principle of conservation of angular momentum

Ans: The angular speed of combination is 250 r.p.m.
Example – 11:
Two wheels of moments of inertia 4 kg m2 and 2 kg m2 rotate at the rate of 120 rev/min and 240 rev/min respectively and in the same direction. If the two are coupled so as to rotate with a common angular velocity, find the speed of revolution.
Given: M.I. of the first wheel = I1 = 4 kg m2, Initial speed of rotation of first wheel = N1 = 120 r.p.m., M.I. of the second wheel = I2 = 2 kg m2, Initial speed of rotation of second wheel = N2 = 240 r.p.m.,
To Find: New frequency of rotation = N =?
Solution:
By the principle of conservation of angular momentum

Ans: The angular speed of combination is 160 r.p.m.
Example – 12:
Two wheels of moments of inertia 4 kg m2 each rotate at the rate of 120 rev/min and 240 rev/min respectively and in the opposite direction. If the two are coupled so as to rotate with a common angular velocity, find the speed of revolution.
Given: M.I. of the first wheel = I1 = 4 kg m2, Initial speed of rotation of first wheel = N1 = 120 r.p.m., M.I. of the second wheel = I2 = 4 kg m2, Initial speed of rotation of second wheel = N2 = 240 r.p.m.,
To Find: New frequency of rotation = N =?
Solution:
As the two wheels are rotating in the opposite direction, the total initial angular momentum is

By the principle of conservation of angular momentum

Ans: The angular speed of combination is 60 r.p.m.
Example – 13:
Two wheels A and B can rotate side by side on the same axle. Wheel A of M.I. 0.5 kg m2 is set spinning at 600 r.p.m. Wheel B of M.I. 2 kg m2 is initially stationary. A clutch now acts to join A and B so that they must spin together. At what speed will they rotate? How does the rotational K.E. before joining compare with the rotational K.E. afterwards?
Given: M.I. of the first wheel = IA = 0.5 kg m2, Initial speed of rotation of first wheel = NA = 600 r.p.m., M.I. of the second wheel = IB = 2 kg m2, Initial speed of rotation of second wheel = NB = 0 r.p.m.,
To Find: New common frequency of rotation = N =?
Solution:

By the principle of conservation of angular momentum

Kinetic energy before coupling

Kinetic energy after coupling

Dividing equation (2) by (1)

Ans: The new angular speed is 120 r.p.m., the ratio of initial K.E. to Final K.E.is 5:1
Previous Topic: Numerical Problems on Moment of Inertia
Next Topic: Numerical Problems on Angular Momentum
2 replies on “Angular Momentum”
Nice answering
I like to give lots of thank you . For providing such impotant question from exam poit of view . Detail solution help me alot to understand concept also.