Science > Physics > Electrostatics > Electric Potential
Electric Potential at a Point:
The electric potential at any point in the electric field is defined as the work that must be done by the external force to move unit positive charge from infinity to that point without acceleration.
If W is the work done in moving the charge qo from infinity to the point in the electric field. Then the potential at that point is given by
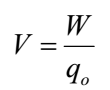
The S.I. unit of potential difference is volt (V).
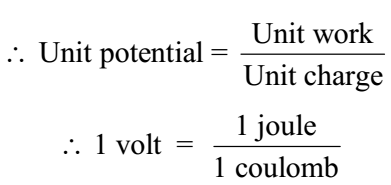
The electric potential at a point in electric field is said to be 1 volt, if 1 joule of work is done, against an electric intensity, to bring a charge of 1 coulomb from infinity to that point.
The Concept of Potential Difference:
The electric potential difference between two points A and B in an electric field is work done in moving a unit positive charge without acceleration from A to B.
Explanation:
Consider charge (+q) kept in the medium of dielectric constant K. It will create an electric field around it. If another charge is kept in this field then it will always experience a force. Hence to move the charge in the electric field from one point to another some work has to be performed. The potential difference between points A & B is defined as work done (WAB) in moving unit positive charge from point A to point B without acceleration. Let q0 be the +ve charge kept in the electric field created by charge +q. The potential difference between two points A & B is given by
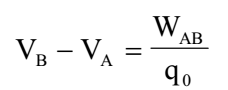
The potential difference between two points in the electric field is said to be 1 volt if 1 joule of work is done in moving a charge of 1 coulomb from a point at lower potential to a point at higher potential without acceleration.
The Expression for Electric Potential at a Point:
Consider charge (+q) kept in the medium of dielectric constant k. It will create an electric field around it. If another charge is kept in this field then it will always experience a force. Hence to move the charge in the electric field from one point to another some work has to be performed. The potential difference between points A & B is defined as work done (W AB) in moving unit positive charge from point A to point B without acceleration. Let q0 be the +ve charge kept in the electric field created by charge +q. The potential difference between two points A & B is given by


Let P be the point at a distance ‘r’ from charge +q. Let q0 be the charge kept at point P. The force F acting on charge q0 is away from charge +q and along vector OP. The electric intensity at point P is given by

By force F the charge q0 is repelled. To move charge from A to B we have to apply equal and opposite force which to given by

The work done by this force against repulsive force to move charge from very small distance is given by

Total work done in moving the charge from A to B can be found by integrating the above equation.



This is an expression for the potential difference between two points A & B in the electric field.
Now, potential at a point is defined as work done in moving unit +Ve charge from infinity to that point without acceleration
∴ rA = ∞
let, rB = r
∴ VB = V and VA = 0

This is an expression for potential at a point in the electric field.
Electron Volt:
Electron volt is a unit of energy used in atomic and nuclear physics. The kinetic energy acquired by the an electron, when it is accelerated through a potential difference of 1 volt in vacuum is called one electron volt (1 eV).
Relation Between electron volt and joule:
When a charge moves through the electric field work is done which is given by
Work done = charge x potential difference
This work done is converted into kinetic energy of charge
kinetic energy of charge = charge x potential difference
1 electron volt = Charge on one electron x 1 volt
1 eV = 1.6 x 10-19 joule
This is the relation between the electron volt and joule.
Relation Between Electric Intensity and Potential:
Let us consider uniform electric field of intensity . In uniform electric field the lines of force are equispaced and parallel to each other. Let A and B two points situated in this electric field such that line joining the two points is parallel to the direction of electric field. Let d be the distance between the two points.
Let us consider a test charge q0 kept at point O. Then the force acting on this charge in electric field is given by. The direction of this force is same as that of the electric field i.e. downwards. To move the charge from A to B without acceleration in the electric field we have to apply equal and opposite force given by
. Thus the direction of this force is upward.

Let us assume this force moves the charge q0 from A to B through a small distance. Then, the work done is given by

The total work done can be calculated by integrating above equation.


This is the relation between electric intensity and potential in uniform electric field.
Electric Dipole and Electrical Dipole Moment:
Consider two equal and opposite charges say +q & -q separated by some finite distance ‘2a’ then the two charges are said to form what is called as an electric dipole. The dipole consists of two equal and opposite charges, hence the total charge of the dipole is zero, but it still exhibits electrical properties due to the separation of the charges.

The electric dipole movement is given by

Considering magnitude only,
p = q. 2a
Electric dipole movement is the vector quantity whose direction is from negative charge to positive charge.
Electric Flux.
- The total number of electric lines of force passing normally though a given area in an electric field is called the electric flux though that area.
- Consider an infinitesimal area (very small area) ds drawn in an electric field. Let
E be the electric intensity at the centre of this area. The area ds is so small that the intensity at every point of this area can be assumed to be the same as E. The area ds can be represented by a vector drawn perpendicular to it. Let q be the angle between
E and ds
.

Then the electric flux (Φ) through the area ds is given by the relation.
Φ = E ds cos θ

Unit of Electric Flux
We have Φ = E ds cos θ
Thus, Unit of Φ = unit of E x unit of ds
Unit of Φ= V/m x m2
Unit of Φ = Vm