Magnetic Induction and Potential at any Point

Science > Physics > Magnetism > Magnetic Induction and Magnetic Potential at any Point

In this article, we shall study to derive an expression for magnetic induction and magnetic potential at any point in a magnetic field created by a bar magnet.

Magnetic Induction at Any Point Due to a Short Bar Magnet:

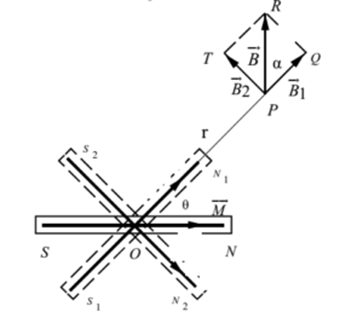
Consider a short magnetic dipole NS.  Let  be the magnetic moment of the dipole

M = m x 2l ………………(1)

The direction of magnetic induction is along the axis from S-pole to N-pole inside the magnet.

Consider a point ‘P’ near the dipole at distance ‘r’ from its centre O. i.e. OP = r Let ‘ θ’ be the angle between the line joining the point from the centre O and the axis of the dipole (angle between OP and SN). Resolving magnetic moment into two mutually perpendicular components, we have,  the component M Cosθ along OP and M Sinθ perpendicular to OP.

Now, the point P lies on the axis of M Cosθ. Hence, the magnetic induction at, the axis point of M Cos θ is given by

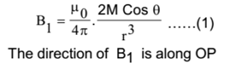
Also, the given point P lies on the equatorial-line of component M Sin θ. Hence, the magnetic induction at the equatorial point of M Sin θ is given by

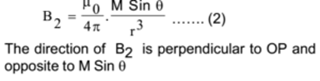
Let B₁ and B₂ be represented by sides PQ and PT of completed parallelogram PQRT. The diagonal PR represents the resultant magnetic induction in magnitude and direction.

This is the magnitude of the resultant induction B at point P.

Let ∝ be the angle made by the resultant B with the direction of OP

This is the angle made by B with OP.  Hence, the total inclination of the resultant induction B with the axis of the dipole is  ( θ + ∝ )

Special cases:

Case 1: If P is a point on the axis of the dipole, then θ = 0° or θ = 180° and Cos θ = ± 1

Case – 2: If P is a point on the equator of the dipole, then θ = 90° and Cos θ = 0

Magnetic Potential at Any Point Due to a Short Bar Magnet:

The magnetic potential at a point in a magnetic field is defined as the work done in moving unit north pole from infinity to that point. It is denoted by ‘V’ and its S.I. unit is J/Am or Wb/m.

In free space, the magnetic potential at a point due to the magnetic pole of strength ‘m’ units and at a distance, r is given by

Consider a short magnetic dipole NS.  Let M be the magnetic moment of the dipole

M = m x 2l ………………(1)

The direction of M is along the axis from S-pole to N-pole.

Consider a point ‘P’ near the dipole at distance ‘r’ from its centre O. i.e. OP = r. Let ‘θ’ be the angle between the line joining the point from the centre O and the axis of the dipole (angle between OP and SN).

Now the magnetic potential due to the North Pole of a magnetic dipole is given by

The magnetic potential due to the North Pole of a magnetic dipole is given by

Since the magnetic potential is a scalar quantity, the resultant potential at a point P is given by

Case 1: If P is a point on the axis of the dipole, then θ = 0° or θ = 180° and Cos θ = ± 1

Case – 2: If P is a point on the equator of the dipole, then θ = 90° and Cos θ = 0

Hence V_equator = 0

Science > Physics > Magnetism > Magnetic Induction and Magnetic Potential at any Point