Science > Physics > Nuclear Physics > Nuclear Structure
In this article, we shall discuss the composition of nucleus and concept of nuclear radius, nuclear vlume, and nuclear density.
Geiger Marsden Experiment:
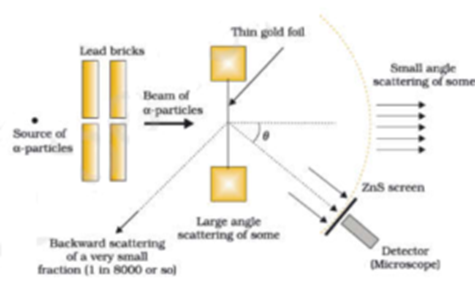
A narrow beam of alpha particles from the radioactive source was incident on a thin gold foil. The scattering of alpha particles takes place. The scattered alpha particles were detected by a detector fixed on a stand. The deviation of alpha particles from their original path is called the scattering angle. They observed that most of the alpha particles just passed through without any deviation as if there is empty space. A few alpha particles were deflected through smaller angles. A few alpha particles deviated through larger angles. This larger deflection is possible only if alpha-particles collide with heavy and positively charged particles inside the atom because like charges only repel each other. This massive +ve charge is at the centre of the atom and called the nucleus. Very few alpha particles were rebounded i.e. they deviated through 180°. This concludes that the nucleus is very small as compared to the volume of the atom.
Rutherford’s Model of an Aom:
From the observations of the above experiment, Rutherford put forward the concept of his atomic model. The atom consists of a centrally located positively charged nucleus. The whole mass of an atom is concentrated in the nucleus. Around the nucleus, there is empty space in which the negatively charged electrons revolve in different orbits. The total positive charge of the nucleus is equal to the total negative charge on orbiting electrons. Hence atom is electrically neutral. Rutherford’s model of an atom is also called as a planetary model of an atom.
From the x-ray technique, it is observed that the charge on the nucleus is Ze and it is positive. Where e is the magnitude of the charge on one electron. Thus it was considered that the nucleus consists of z number of positively charged particles. Each particle carries a charge of + e. These particles are termed as protons. In 1932 Chadwick proved the existence of neutral particles in the nucleus. These neutral particles are called neutrons. The mass of neutron and proton is almost the same.
Nucleus of Hydrogen is an exception because it contains only one proton and no neutron. The lightest positive charge found had the mass of the hydrogen atom and carried a positive charge equal to the electronic charge. This led to the idea that all atoms were made up from hydrogen hence the name proton (which comes from the Greek word protos which means first) was given to indicate its importance.
In an atom total number of protons in neutron is equal to the number of electrons in the atom. Hence total amount of positive charge on nucleus is balanced by total charge on electrons. Hence as a whole atom is electrically neutral.
Nucleus of different elements are different and has unique composition. Size of nucleus is of an order of 10-14 m.
Constituents of Nucleus:
The particles protons and neutrons present in the nucleus are collectively called as the nucleons. The number of protons present in the nucleus of an atom is called the atomic number. It is denoted by the letter ‘Z’. The number of neutrons present in the nucleus of an atom is known as the neutron number. It is denoted by ‘N’. The total number of protons and neutrons present in the nucleus of an atom of the element is called the mass number. The mass number is denoted as ‘A’.
A = Z + N or N = A – Z
The mass of an atom is measured in a unit called atomic mass unit (a.m.u.)
Proton-Electron Hypothesis:
Before the discovery of Neutron by Chadwick in 1932, it was considered that proton and electron were constituent particles of nucleus. This consideration was based on following hypothesis:
- During radioactive decay, beta particles are emitted and they were proved to be fast moving electrons.
- As atom is electrically neutral If A is atomic mass of an element, then it should contain ‘A’ number of protons and (A – Z) electrons in the nucleus. Where Z is number of positive charge in nucleus (number of protons).
- Also Z no. Electron outside the nucleus i.e equal no. of protons and electrons in an atom, some electrons inside and some electrons outside the nucleus. Thus in helium nucleus 2He4, there are 4 protons and 2 electrons in the nucleus. Two compensate the extra positive charge this hypothesis assume there are 2 more electrons which revolve around the nucleus.
- This theory was suitable to explain emission of alpha and beta particles by radioactive element.
Shortcoming of Proton-Electron hypothesis:
According to Heisenberg’s uncertainty principle, if an electron is to exist inside the nucleus, it should have energy of at least 200 MeV. But beta particles (fast moving electrons emitted by radioactive element) do not have kinetic energy more than 4 MeV, Thus on the basis of wave mechanics, the existence of electron in the nucleus cannot be justified.
The experimental values of angular momentum of nuclei differ widely from the calculated values on the basis of proton-electron hypothesis.
If electron exist in nucleus the nuclear magnetic moment cannot be less than the magnetic moment of electron. But the magnetic moment of nucleus is only about one thousandth times that of electron. Hence electron cannot be a constituent of nucleus.
Proton-Neutron Hypothesis:
This hypothesis was proposed by Chadwick after the discovery of neutron in 1932.
A nucleus of mass number ‘A’ and atomic number ‘Z’, contains Z protons and ‘A – Z’ no. of neutrons inside the nucleus. ‘Z’ no. of electrons are revolving around the nucleus. Thus the atom is electrically neutral.
Merits of Proton-Neutron Hypothesis:
- The existence of neutron in nucleus satisfies the Heisenberg’s uncertainty principle.
- It explains the emission of beta particles from radioactive nuclei, as a result of inter conversion of proton and neutron
- It solves the problem of nuclear spin. Nuclei having odd mass no. will have half integral spin and those with even mass no. will have integral spin.
Size of Nucleus:
The nuclear radius is the distance from the centre of the nucleus at which the density of nuclear material decreases to one-half of its maximum value at the centre. Nucleus has no definite boundary, but its radius is given by following relation:
R = Ro A1/3
Where Ro is constant for all nuclei and its value is 1.2 x 10-15 m
A = Mass number of nucleus
Thus radius of nucleus depends on the mass number of nucleus.
Example 01:
Find size of nucleus of oxygen 8O16.
For oxygen nucleus A = 16
R = Ro A1/3
R = 1.2 x 10-15 x (16) 1/3
R = 3.02 x 10-15 m
Ans: The radius of nucleus of oxygen 8O16is 3.02 x 10-15 m.
Example 02:
The nuclear radius of 8O16 is 3x 10-15 m. What is nuclear radius of 82Pb205?
Given: RO = 3x 10-15 m
To Find: RPb =?
Solution:
We have R = Ro A1/3
Thus R α Ro A1/3
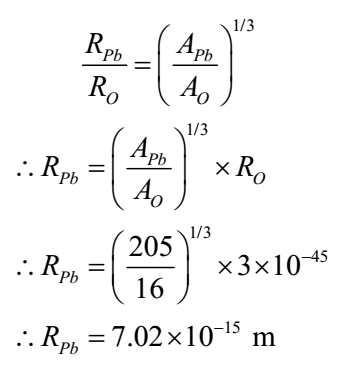
Ans: The radius of lead nucleus is 7.02 x 10-15 m or 7.02 fermi
Example 03:
The nuclear radius of 13Al27 is 3.9 x 10-15 m. What is nuclear radius of 84Po216?
Given: RAl = 3.9 x 10-15 m
To Find: RPo =?
Solution:
We have R = Ro A1/3
Thus R α Ro A1/3

Ans: The radius of polonium nucleus is 7.8 x 10-15 m or 7.8 fermi
Volume of Nucleus:
Volume of nucleus is given by

Thus the volume of the nucleus is directly proportional to the mass number of the nucleus.
Example 04:
Find Volume of nucleus of chlorine 17Cl35.
For chlorine nucleus A = 35
Volume of Nucleus = 7.24 x 10-45 A m3
Volume of Nucleus = 7.24 x 10-45 x 35 m3
Volume of Nucleus = 2.53 x 10-43 m3
Density of Nucleus:

Where m = mass of each nucleon

Notes:
- Nuclear density is independent of mass number of nucleus.
- It is nearly same for all nuclei
- It has very high value. Such high densities can be found in white dwarf stars.
- Its value is not same inside the nucleus. It is maximum at the centre and gradually decreases as we move away from the centre of the nucleus.
- The nuclear radius is the distance from the centre of the nucleus at which the density of nuclear material decreases to one-half of its maximum value at the centre.
Example 05:
Find the density of nuclear mass in 92U238. If Ro = 1.5 fermi and mass of each nucleon = 1.67 x 10-27 kg.

Example 06:
Find the density of nuclear mass hydrogen nucleus. If Ro = 1.2 fermi and mass of each nucleon = 1.67 x 10-27 kg.

Example 07:
Obtain an approximate ratio of radii of the gold isotope 79Au197 and the silver isotope 47Ag107. What is the density of their nuclear densities?
We have R = Ro A1/3
Thus R α Ro A1/3

The nuclear density is independent of mass number of nucleus. Hence ratio of their nuclear densities is 1.
Ans: The approximate ratio of radii of the gold isotope 79Au197 and the silver isotope 47Ag107 is 1.225 and the ratio of their nuclear densities is 1.