Science > Physics > Units and Measurement > Measurement of Length, Area, and Volume > Distances of Heavenly Bodies from the Earth
In this article, we shall study the parallax and other methods to find the distance between two heavenly bodies.
Parallax:
Hold a pencil vertically in front of you at a certain distance against a point on a background like a wall. Now view the pencil through your left eye closing your right eye and then view the pencil through your right eye closing your left eye. You will notice that with respect to the fixed point on the wall the position of the pencil is changing. This phenomenon is known as parallax. The distance between the two points of observation is called the basis. In this example, the basis is the distance between the eyes.
Parallax is defined as the apparent shift of a body with respect to another, with the shift of eye. The distances between planets and stars from the Earth cannot be measured directly with a metre scale. Hence indirect method called the parallax method is used.
Example – 01:
Calculate the angle of a) 1O (degree) b) 1’ (minute of arc or arcmin) and c) 1’’ (second of arc or arc second) in radians.
Solution:
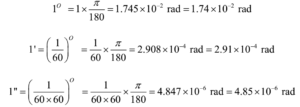
Determination of the Distance Between a Faraway Planet or a Near Star and the Earth (Parallax Method – I):

To measure the distance d of a faraway planet or near star S1 by the parallax method, we observe it from two different positions (observatories) A and B on the Earth, separated by distance b at the same time as shown in Fig. Some distant star S is taken as reference. We measure the angle between the two directions along which the planet is viewed at these two points. The∠ASB called parallax angle = θ = θ1 + θ2, Now the distance d << b.
sinθ = θ = b/d
∴ d = b/θ
θ should be measured in radians.
Determination of the Distance Between a Faraway Planet or a Near Star and the Earth (Parallax Method – II):

To measure the distance d of a faraway planet, the moon or the near star (the sun) S1 by the parallax method, we observe it from two diametrically opposite positions on the earth. A and B on the Earth, separated by distance b at the same time as shown in Fig. Some distant star S is taken as reference. We measure the angle between the two directions along which the planet is viewed at these two points. The∠ASB called parallax angle = θ = θ1 + θ2, Now the distance d << b.
b = AB = 2R = 2 x radius of earth
sinθ = θ = b/d
∴ d = b/θ
θ should be measured in radians.
Example – 02:
The moon is observed from two diametrically opposite points A and B on Earth. The angle θ subtended at the moon by the two directions of observation is 1°54’. Given the diameter of the Earth to be about 1.276 x 107 m, compute the distance of the moon from the Earth.
We have θ = 1O54’ = 1 x 60’ + 54 = 114’
θ = 114’ x 2.91 x 10-4 = 3.32 x 10-2 rad
Also b = AB = diameter of earth = 1.276 x 107 m

Ans: The distance of the moon from the earth is 3.84 x 105 km
Example – 03:
Two parallax of a heavenly body measured from two points diametrically opposite on equator of Earth is 2.0′. Calculate the distance of the heavenly body if the radius of the earth is 6400 km.
We have θ = 2’ = 2 x 2.91 x 10-4 = 5.82 x 10-4 rad
Also b = AB = diameter of earth = 2 x 6400 km = 12800 km
Now, d = b/θ = 12800 / 5.82 x 10-4
d = 2.2 x 107 km = 2.2 x 1010 m
Ans: The distance of the heavenly body from the earth is 2.2 x 1010 m
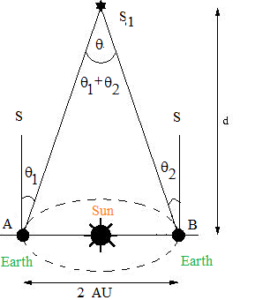
Determination of The Distance of a Faraway Planet or a Near Star from the Earth (Parallax Method – III):
To measure the distance d of a faraway planet or the near star S1 by the parallax method, we observe it from two diametrically opposite positions on the earth’s orbit around the sun at a time gap of six months. A and B on the Earth’s orbit, separated by distance b as shown in Fig. Some distant star S is taken as reference. We measure the angle between the two directions along which the planet is viewed at these two points. The∠ASB called parallax angle = θ = θ1 + θ2, Now the distance d << b.
b = AB = 2 AU = 2 x 1.496 x 1011 m
sinθ = θ = b/d
∴ d = b/θ
θ should be measured in radians.
Example – 04:
When the observations are taken at an interval of 6 months, the angle of parallax for star is 0.4’’. Find the distance of star in light year and parsec.
θ = 0.44’’ = 0.4 x 4.847 x 10-6 = 1.939 x 10-6 rad

Ans: The distance of the star from the earth is 16.3 lightyears or 5 parsec.
Determination of Diameter of the Moon or the Sun:

The angular diameter of the moon (or the sun) is the angle subtended by two diametrically opposite ends of the moon (or the sun) at a point on the Earth.
Let D be the diameter of the moon (or the sun) and d be the distance between the moon (or the sun) from the earth. D << d
arc length AB = D = d θ
θ should be measured in radians.
Example – 05:
The Sun’s angular diameter is measured to be 1920”. The distance D of the Sun from the Earth is 1.496 × 1011 m. What is the diameter of the Sun?
Sun’s angular diameter θ = 1920″ = 1920 x 4.85 x 10-6
= 9.31 x 10-3 rad
Sun’s diameter = D = d θ
d = (1.496 × 1011) x (9.31 x 10-3 ) = 1.39 x 109 m
Ans: The diameter of the sun is 1.39 x 109 m
Example – 06:
The angle subtended by the Moon at a point on the Earth is 0o31’. If the distance of the Moon from the Erath is 3.84 x 105 km, find the diameter of the moon.
θ = 0o31’ = 31 x 2.908 x 10-4 = 9.01 x 10-3 rad
Now D = d θ = 3.84 x 105 x 9.01 x 10-3 = 3.46 x 103 km
Ans: Diameter of the moon is 3.46 x 103 km
Determination of Angular Distance Between Two Stars:

Let θ1 be the elevation of a distant star S1 and θ2 be the elevation of another distant star S2 such that (θ2 > θ1). Then the quantity (θ2 – θ1) is called the angular distance between the stars.
It is to be noted that the smaller angular distance between two distant stars does not imply that the two stars are close to each other. There is a possibility that distance between them is very very large (hundreds of light-years).
Determination of the Distance of Inferior Planets from the Earth (Copernicus Method):
The planets which are closer to the Sun than the Earth are called inferior planets. The Mercury and Venus are two inferior planets. Copernicus assumed the orbits of inferior planets as perfectly circular.

The angle formed at the Earth between the Earth planet direction and the Earth-Sun Direction is called the planet elongation and is denoted by symbol ε. The planets elongation changes continuously. When elongation acquires maximum value it appears to be farthest from the sun, At this time the Sun and the Earth subtends an angle of 90° at the planet. This maximum elongation is noted.
SE = 1 AU = 1.496 x 1011 m
Δ EPS is a right-angled triangle
sin ε = SP/ SE
∴ SP = SE sin ε
Example – 07:
Copernicus assumed the orbit of Mercury to be circular and estimated its orbital radius as 0.38 AU. Using this radius derive angle of maximum elongation for mercury and its distance from the Earth when the elongation is maximum.
We have SP = SE sin ε
Where SP = orbital radius of Planet = 0.38
SE = orbital radius of the Earth = 1 AU
0.38 = 1 x sin ε
ε = sin-1(0.38) = 22°20′
Applying Pythagoras theorem to ΔEPS
SE2 = EP2 + SP2
∴ EP2 = SE2 – SP2
∴ EP2 = (1)2 – (0.38)2 = (1+0.38)(1-0.38)
∴ EP2 = 1.38 x 0.62 = 0.8556
∴ EP = 0.925 AU
∴ EP = 0.925 x 1.496 × 1011 m = 1.384 × 1011 m
Ans: The angle of maximum elongation for Mercury is 22°20′ and the distance between the Earth and Mercury at maximum elongation is 1.384 × 1011 m
Example – 08:
For Venus the angle of maximum elongation is found to be approximately equal to 47°. Determine the distance between the Sun and Venus and that between the Erath and the Venus. Also, find orbital period of Venus.
We have SP = SE sin ε
Where SP = orbital radius of Planet
SE = orbital radius of the Earth = 1 AU
SP = 1 x sin 47° = 1 x 0.7314 = 0.7314 AU
∴ SP = 0.7314 x 1.496 × 1011 m = 1.094 × 1011 m
Applying Pythagoras theorem to ΔEPS
SE2 = EP2 + SP2
∴ EP2 = SE2 – SP2
∴ EP2 = (1)2 – (0.73)2 = (1+0.73(1-0.73)
∴ EP2 = 1.73 x 0.27 = 0.4671
∴ EP = 0.6834 AU
∴ EP = 0.6834 x 1.496 × 1011 m = 1.022 × 1011 m

Ans: The distance between the sun and venus is 1.094 × 1011 m and the distance between the Earth and Venus at maximum elongation is 1.022 × 1011 m, Period of Venus is 226 days
Determination of the Distance of Superior Planets from the Sun:
The planets which are farther to the Sun than the Earth are called inferior planets. The Mars, The Jupiter, The Saturn, The Neptune and The Uranus are superior planets.
By Keppler’s period law of orbiting satellite “The square of the time period of the satellite is directly proportional to the cube of the semimajor axis of the orbit.
Example – 09:
A Period of a planet orbiting around the sun is half that of the earth. What is the orbital radius of the planet?

∴ rP = 0.63 x 1.496 × 1011 m = 9.42 × 1010 m
Thus rP/ rE = 0.63/1 = 0.63
Ans: The orbital size of the planet is smaller than that of the Earth by a factor of 0.63
Measurement of Distances of Star by Intensity Method (Optical or Spectroscopic Method):
This method uses the inverse square law of photometry, it states that “The intensity of illumination at a point varies inversely as the square of the distance from the source of light
Thus I ∝ 1/r2

This method is used to find the distance of a star from the earth. The assumption of this method is the intrinsic brightness of all the stars is the same. This method gives the approximate result.
In the above formula, I1 is the apparent brightness of a star at a distance r1 from the earth and I2 is the apparent brightness of a star at a distance r2 from the earth. If we know the intensity ratio and the distance of one star from the earth, the distance of another star from the earth can be calculated.
Measurement of Distances of Star by Doppler Shift Method (Optical or Spectroscopic Method):
When a body that is emitting radiation has a non-zero velocity relative to an observer, the wavelength of the emission will be shortened or lengthened, depending upon whether the body is moving towards or away from an observer. This change in observed wavelength or frequency is known as the Doppler shift.
If the object is moving towards an observer, then the emission will be blueshifted – i.e. the wavelength of the emission will be shortened, moving it towards the blue end of the spectrum. If the object is moving away from an observer, then the emission will be redshifted i.e. the wavelength of the emission will increase, moving it towards the red end of the spectrum.
Generally, by determining the redshift and using doppler’s formulae the distance of the star and its speed at which it is moving away from the earth can be found.
For More Topics in Measurement of Length, Area, and Volume Click Here
One reply on “Distances of Heavenly Bodies from the Earth”
All notes are very good