Thermodynamic or Temperature Scales

Science > Physics > Thermal Properties of Matter and Thermodynamics > Thermodynamic or Temperature Scales

In last article, we have studied the concept of temperature. In this article, we shall discuss different thermodynamic or temperature scales.

Temperature can be defined in several ways:

• The temperature may be defined as the degree of hotness or coldness of a body.
• The temperature of a body is an indicator of the average thermal energy (Kinetic energy) of the molecules of the body.
• It is that physical quantity which decides the flow of heat in bodies brought in contact. Heat always flow from the body at higher temperature to the body at the lower temperature.

It is measured in °C (centigrade or Celsius) or K (Kelvin). It is measured by a device called a thermometer. The common thermometer is a mercury thermometer.

The branch of Physics that deals with the measurement of temperature is called Thermometry.

Concept of Thermal Equilibrium:

Two bodies are said to be in thermal equilibrium with each other if no transfer of heat takes place when they are brought in contact, clearly, the two bodies are at the same temperature.

Characteristics of Thermal Equilibrium:

When two or more bodies are kept in contact and they are at the same temperature and there is no transfer of heat taking place between them, then those bodies are said to be in thermal equilibrium with each other. If thermal equilibrium does not exist, then heat flows from a body at a higher temperature to the body at a lower temperature, till thermal equilibrium is established.  Characteristics define thermal equilibrium are as follows:

• Equal Temperatures: In thermal equilibrium, all objects or systems involved have the same temperature. Temperature is a measure of the average kinetic energy of the particles within a substance. When objects are in thermal equilibrium, their average kinetic energies are the same.
• No Net Heat Transfer: In thermal equilibrium, there is no net transfer of heat between the objects or systems. Thus, there is no heat transfer between the bodies due to conduction or convection. This means that while individual particles may still exchange energy through collisions, the overall transfer of thermal energy between the objects results in no net change in their temperatures.
• Stable State: Thermal equilibrium represents a stable state in which the thermal properties of the objects or systems involved remain constant over time. Any initial differences in temperature between the objects or systems will eventually lead to thermal equilibrium as heat is transferred between them.
• Zero Temperature Gradient: A temperature gradient refers to the change in temperature over a distance. In thermal equilibrium, there is no temperature gradient between the objects or systems. This means that the temperature is uniform throughout the system.
• Dynamic Equilibrium: While there is no net transfer of thermal energy in thermal equilibrium, individual particles within the system may still be in motion, exchanging energy through collisions. Thermal equilibrium represents a dynamic balance where the rates of energy transfer between particles are equal.

Understanding thermal equilibrium is crucial in various fields such as thermodynamics, heat transfer, and the study of thermal properties of materials. It helps in analyzing and predicting the behaviour of systems where heat exchange is involved.

Zeroth Law of Thermodynamics:

The Zeroth Law of Thermodynamics is one of the fundamental principles that govern thermodynamic systems. It was formulated after the First and Second Laws of Thermodynamics, but its importance in establishing temperature measurement and the concept of thermal equilibrium led to its designation as the “Zeroth” law. This law introduces the concept of hotness and coldness which leads to the concept of the temperature of a body.

The Zeroth Law states that “If two systems are each in thermal equilibrium with a third system, then they are in thermal equilibrium with each other.”

Thus, if two bodies P and Q are in thermal equilibrium and also P and R in thermal equilibrium then Q and R, are also in thermal equilibrium.

The Zeroth Law essentially establishes the concept of temperature and allows us to define and measure it. It provides a basis for the construction of thermometers and temperature scales. For instance, if two objects are in thermal equilibrium, they have the same temperature.

The importance of the Zeroth Law lies in its role in defining the concept of temperature and establishing the foundation for thermal equilibrium. It allows us to compare temperatures and define scales, which are fundamental for understanding and analyzing the behaviour of thermodynamic systems.

Triple Point of Water:

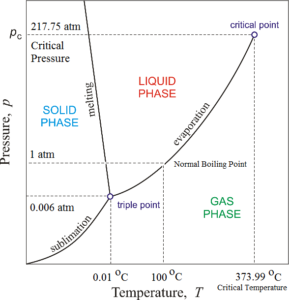
Phase diagram of water consists of three curves sublimation curve, evaporation curve and melting curve meeting each other at a point called the triple point. Due to these curves, the phase diagram has three regions

The region to the left of the melting curve and above the sublimation curve represents the solid phase of water i.e. ice. The region to the right of the melting curve and above the evaporation curve represents the liquid phase of water i.e. water. The region below the sublimation curve and evaporation curve represent the gaseous phase of water i.e. vapours.

A curve on the phase diagram represents the boundary between two phases of the two substances. Along any curve, the two phases can coexist in equilibrium.

Along the melting curve, ice and water can remain in equilibrium. This curve is called a fusion curve or ice line. This curve indicates that the melting point of ice decreases with an increase in pressure. Along the evaporation curve, water vapours and water can remain in equilibrium. This curve is called the vaporisation curve or steam line. This curve indicates that the boiling point of water increases with an increase in pressure. Along the sublimation curve, ice and water vapours can remain in equilibrium. This curve is called the sublimation line or hoar frost line.

The three curves meet each other at a single point at A. This common point is known as the triple point of water. At the triple point of water can coexist in all the three states in equilibrium. The triple point of water corresponds to a pressure of 0.006023 atmospheres and temperature (0.01 °C) 273.16 K.

Significance of Triple Point of Water:

• Triple point temperature of the water is the temperature at which water can coexist in all the three states viz. Ice (solid), water (liquid), vapours (gas) in equilibrium.
• This triple point temperature of the water is used for defining the absolute temperature scale. In absolute or Kelvin scale 0 K is considered as the lower fixed point while the triple point temperature of the water is taken as the upper fixed point.
• Thus one kelvin temperature corresponds to 1/273.16 of the triple point temperature.

Various Temperature Scales:

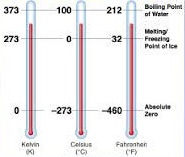
There are several temperature scales used around the world, each with its own reference points and units of measurement. Here are the most common temperature scales:

Celsius Scale (° C):

In this scale, the melting point of ice at one-atmosphere pressure and at mean sea level is taken as the lower reference point and consider as 0° C. While boiling point of water at one atmosphere pressure and at mean sea level is taken as an upper reference point and consider as 100° C. The range between the two reference points is divided into 100 equal parts and each part is called 1° C (one degree Celsius). This scale is also called a centigrade scale.

A lower limit of 0° C is considered arbitrary, this scale can be extended to indicate negative temperatures also. A temperature below -273.15° C is not possible.

Fahrenheit Scale (° F):

In this scale, the melting point of ice at one-atmosphere pressure and at mean sea level is taken as the lower reference point and consider as 32° F. While boiling point of water at one atmosphere pressure and at mean sea level is taken as the upper reference point and consider as 212° F. The range between the two reference points is divided into 180 equal parts and each part is called 1° F (one degree Fahrenheit). Nowadays, this scale is not in use.

Kelvin Scale (K):

In this scale, the lowest possible temperature -273.15° C  is taken as a lower reference point. This temperature is called absolute zero. The division of 1 K is equal to 1° C. The unit of temperature in the kelvin scale is K (kelvin) and is considered as the fundamental unit in the S.I. system of units.

Reaumer Scale:

In this scale, the melting point of ice at one-atmosphere pressure and at mean sea level is taken as the lower reference point and consider as 0° R. While boiling point of water at one-atmosphere pressure and at mean sea level is taken as an upper reference point and consider as 80° R. The range between the two reference points is divided into 80 equal parts and each part is called 1° R (one-degree Reaumer).

Conversion of Temperature in Different Scales:

Celsius scale to Kelvin scale  ° C  +  273 = K

Kelvin scale to Celsius scale  K  –  273 = ° C

Numerical Problems:

Example 01:

Find the temperature at which the temperature scales in the following pairs give the same reading: (1) Celsius and Fahrenheit and (2) Fahrenheit and Kelvin

(1) Celsius and Fahrenheit

Solution:

Let θ be the required temperature, such that F = C = θ .

We have

∴ (θ – 32)/180 = θ /100

∴ 100θ – 3200 = 180 θ

∴ – 80θ = 3200

∴ θ = – 40^oF = – 40^oC

Ans: Thus at – 40^oC or – 40^oF, the temperature scales in Celsius and Fahrenheit give the same reading.

(2) Fahrenheit and kelvin:

Solution:

Let θ be the required temperature, such that F = K = θ .

We have

∴ (θ – 32)/9 = ( θ – 273)/5

∴ 5θ – 160 = 9 θ – 2457

∴ 4θ = 2297

∴ θ = 574.25^oF = 574.25 K

Ans: Thus at 574.25^oF or 574.25^oK, the temperature scales in Fahrenheit and Kelvin give the same reading.

Example 02:

Determine the temperature on the Fahrenheit scale which is indicated by double the number on the Centigrade scale.

Solution:

Let θ be the required temperature in centigrade scale, such that C = θ and F = 2 θ .

We have

∴ (2 θ – 32)/180 = θ /100

∴ 200 θ – 3200 = 180 θ

∴ 20 θ = 3200

∴ θ = 160^oC

∴ 2 θ = 2 x 160^o = 320 ^oF

Ans: 320 ^oF is the temperature on the Fahrenheit scale which is indicated by double the number on the Centigrade scale (160^oC).

Example 03:

Convert the following temperature in centigrade into Fahrenheit

• -37 ^oC

Given C = -37 ^oC

∴ (F – 32)/180 = (-37)/100

∴ 100F – 3200 = 6660

∴ 100F = 9860

∴ F = 98.6^oF

Ans: Thus equivalent of temperature -37 ^oC is 98.6 ^oF

• 100^oC

Given C = -100 ^oC

∴ (F – 32)/180 = 100/100

∴ (F – 32)/180 = 1

∴ F – 32 = 180

∴ F = 212^oF

Ans: Thus equivalent of temperature 100 ^oF is 212 ^oF

• -192 ^oC

Given C = -192 ^oC

∴ (F – 32)/180 = (-192)/100

∴ 100F – 3200 = – 34560

∴ 100F = – 31360

∴ F = – 313.6^oF

Ans: Thus equivalent of temperature -192 ^oC is – 313.6 ^oF

Example 04:

Convert the following temperature in centigrade into Fahrenheit

• -108

Given F = -108 ^oF

∴ (-108 – 32)/180 = C/100

∴ -140/180 = C/100

∴ C = (7/9) x 100

∴ C = – 77.78 ^oC

Ans: Thus equivalent of temperature -108 ^oF is – 77.78 ^oC

• 176

Given F = 176 ^oF

∴ (176 – 32)/180 = C/100

∴ 144/180 = C/100

∴ C = (4/5) x 100

∴ C = 80 ^oC

Ans: Thus equivalent of temperature 176 ^oF is 80 ^oC

• 140

Given F = 140 ^oF

∴ (140 – 32)/180 = C/100

∴ 108/180 = C/100

∴ C = (3/5) x 100

∴ C = 60 ^oC

Ans: Thus equivalent of temperature 140 ^oF is 60 ^oC

Example 05:

The fundamental interval of a thermometer is arbitrarily divided into 80 divisions. The lower fixed point of the thermometer is marked 10 ^o. Find what reading this thermometer will show when the reading on a centigrade thermometer is 60 ^oC.

Solution:

Scale 1: Number of Divisions = n = 80, the lower Fixed Point = L = 10^o.

Centigrade Scale: Number of divisions = n = 100, the lower fixed point = L = 0^o.

Given C = 60^oC

∴ ( θ – 10)/4 = 60/5

∴ ( θ – 10)/4 = 12

∴ ( θ – 10) = 48

∴ θ = 58^o on the new scale

Ans: Thus equivalent of temperature 60 ^oC is 58^o on the new scale.

Example 06:

The lower fixed point of a thermometer is marked 10^o and the upper fixed point is 130^o, the interval between the fixed points is divided into 120 equal divisions. What should be the reading indicated by this thermometer when a Centigrade thermometer reads 40^o?

Solution:

Scale 1: Number of Divisions = n = 120, the lower Fixed Point = L = 10^o., The upper fixed point = U = 130^o

Centigrade Scale: Number of divisions = n = 100, the lower fixed point = L = 0^o.

Given C = 60^oC

∴ ( θ – 10)/6 = 40/5

∴ ( θ – 10)/6 = 8

∴ ( θ – 10) = 48

∴ θ = 58^o on the new scale

Ans: Thus equivalent of temperature 40 ^oC, is = 58^o on the new scale.

Example 07:

The fundamental interval of a thermometer is divided arbitrarily into 40 equal parts and that of another thermometer 𝑦 into 80 equal parts. If the freezing point is marked 20^o and that of y is marked 10^o, what is the temperature on when y indicates 70^o? What is the temperature in degrees celsius?

Part I:

Solution:

Scale of thermometer x: Number of Divisions = n = 40, the lower Fixed Point = L = 20^o,

Scale of thermometer y: Number of divisions = n = 80, the lower fixed point = L = 0^o.

Given Y = 70^oC

∴ (X – 20)/40 = 70/80

∴ X – 20 = 35

∴ X = 55^o on the scale of thermometer X.

Ans: Thus equivalent of temperature 70 ^o on scale of thermometer y, is = 55^o on the scale of thermometer x.

Part II:

Solution:

Scale on thermometer y: Number of Divisions = n = 80, the lower Fixed Point = L = 0^o.

Centigrade Scale: Number of divisions = n = 100, the lower fixed point = L = 0^o.

Given Y = 70^oC

∴ 70/4 = C/5

∴ C = (70/4) x 5 = 87.5^oC

Ans: Thus equivalent of temperature 70 ^o on the scale of thermometer y, is = 87.5^oC on the centigrade scale.

Example 08:

Two arbitrary scales A and B have triple points of water defined on 200 A and 350 B. What is the relation between T_A and T_B?

Solution:

The triple point of water is 373 K

For Scale A, 273 K = 200 A i.e. 1 K = (273/200) T_A …………… (1)

For Scale B, 273 K = 350 B i.e. 1 K = (273/350) T_B …………… (2)

From relations (1) and (2) we have

(273/200) T_A = (273/350) T_B

∴ 350 T_A = 200 T_B

∴ T_A / T_B = 200/350

∴ T_A / T_B = 4/7

Ans: T_A / T_B = 4/7

Example 09:

A Centigrade thermometer has its lower and upper fixed points marked – 0.5 ^oC and 100.5 ^oC. What is the true temperature when this thermometer reads30^oC? The bore of the thermometer is uniform.

Solution:

Scale 1: The lower Fixed Point = L = – 0.5 ^oC., the upper fixed point = U = 100.5 ^oC

Centigrade scale: Number of divisions = n = 100, the lower fixed point = L = 0^o.

Given S = 30^oC

∴ (30 + 0.5)/101= C/100

∴ C = (30.5/101) x 100

∴ C = 30.198^oC

Ans: Thus true temperature reading is 30.198^oC

Example 10:

A thermometer is fixed points marked as 5 and 95. What is the correct temperature in Celsius when the thermometer reads 59?

Solution:

Scale 1: The lower Fixed Point = L = 5, the upper fixed point = U = 95

Centigrade scale: Number of divisions = n = 100, the lower fixed point = L = 0^o.

Given S = 59

∴ (59 – 5)/90= C/100

∴ C = (54/90) x 100

∴ C = 60^oC

Ans: Thus correct temperature reading is 60^oC

Example 11:

In an arbitrary scale of temperature, water boils a 40 ^oC and boils at 290 ^oC. Find the boiling point of water in this scale if it boils at 62 ^oC.

Solution:

Scale 1: The lower Fixed Point = L = 40 ^oC, the upper fixed point = U = 290 ^oC

Centigrade scale: Number of divisions = n = 100, the lower fixed point = L = 0^o.

Given C = 62^oC

∴ (S – 40)/250 = 62/100

∴ S – 40 = 0.62 x 250

∴ S – 40 = 155

∴ S = 195 ^oC

Ans: Thus the boiling point of water, in the new scale is 195^oC

Example 12:

The distance between the upper and lower fixed point is 80 cm. Find the temperature on the Celsius scale if the mercury level rises to a height 10.4 cm above the lower fixed point.

Scale 1: The lower Fixed Point = L = 0 cm, the upper fixed point = U = 80 cm

Centigrade scale: Number of divisions = n = 100, the lower fixed point = L = 0^o.

Given S = 10.4 cm

∴ 10.4/80 = C/100

∴ 80C = 1040

∴ C = 1040/80 = 13 ^oC

Ans: Thus the temperature on the Celsius scale is 13 ^oC

Example 13:

The temperature of the two bodies differs by 1oC. How much do they differ on the Fahrenheit scale?

Solution:

Differentiating both sides w.r.t. temperature T

Ans: Thus the difference of 1^oC in Celsius scale corresponds to the difference of 1.8oF on the Fahrenheit scale.

For More Topics in Thermal Properties of Matter and Thermodynamics Click Here

For More Topics in Physics Click Here