Bohr’s Model of an Atom

Science > Physics > Atoms, Molecule, and Nuclei > Bohr’s Model of an Atom

In the last article, we have studied Rutherford’s model of an atom, its merits, and demerits. In this article, we shall study Bohr’s Model of an atom, its merits, and demerits.

To overcome the limitations of Rutherford’s model of an atom, Neil Bohr put forward his theory of atom using Planck’s quantum theory. Bohr’s theory is applicable to the hydrogen atom.

Bohr’s Atomic Theory of Hydrogen Atom:

Postulate I (Postulate of Circular Orbit):

In a hydrogen atom, the electron revolves around a circular orbit around the nucleus.  The electrostatic force of attraction between the positively charged nucleus and the negativity charged electron provide necessary centripetal force for circular motion.

The Expression For the First Postulate:

Let m be the mass of an electron revolving around the nucleus in a circular orbit of radius r with a constant speed v round the nucleus.  Let – e and + e be the charges on the electron and the nucleus respectively.

By the first postulate,

Centripetal force =  Electrostatic force

Where ε_o is the electrical permittivity of free space

Postulate – II (Postulate of Selected Orbit):

The electron can revolve only in a certain selected orbit in which the angular momentum of the electron is equal to an integral multiple of nh/2π, where h is the Planck’s constant.  These orbits are called stationary or permissible orbits.  The electron does not radiate energy while revolving in these orbits.

The Expression for the Second Postulate:

Let m be the mass of an electron revolving around the nucleus in a circular orbit of radius r with a constant speed v round the nucleus.

Where, n   =    1, 2, 3………..

n = Principal quantum number

h = Planck’s constant

The integer n is called the principal quantum number and it denotes the number of the orbit.

Postulate –III (Postulate of The Origin of Spectral Lines):

When an electron takes a jump from a higher energy orbit to a lower energy orbit, energy is radiated in the form of a quantum or photon of energy hν, which is equal to the difference of energies of the electron in the two orbits.

Expression for the Third Postulate:

Let E_n and E_p be the energies of an electron in the n^th and p^th orbits respectively (n > p) So when an electron takes a jump from the n^th orbit to the p^th orbit energy will be radiated in the form of a photon or quantum such that

E_n –  E_p = hν

Where ν is the frequency of radiation.

Expression for Radius of Bohr’s Orbit:

Let m be the mass of an electron revolving in a circular orbit of radius r with a constant speed  v around the nucleus.  Let – e and + e be the charges on the electron and the nucleus, respectively.

By the first postulate,

Centripetal force =  Electrostatic force

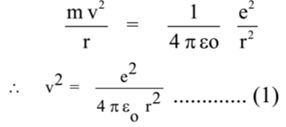
Where ε_o is the electrical permittivity of free space

From the second postulate of Bohr’s theory

From equation (1) and (2)

This is the required expression for the radius of Bohr’s orbit. Since ε_o, h, π, m, e are constant

∴  r    ∝   n²

Thus the radius of the Bohr’s orbit of an atom is directly proportional to the square of the principal quantum number.

The Expression for Velocity of Electron in Bohr’s orbit:

From the second postulate of Bohr’s theory

Where, n = 1, 2, 3………..

n = Principal quantum number

h = Planck’s constant

This is the required expression for the velocity of the electron in Bohr’s orbit of an atom. Since ε_o, h, π, e are constant

∴   v  ∝ 1 / n

Thus the velocity of the electron in Bohr’s orbit of an atom is inversely proportional to the principal quantum number.

The Expression for Angular Velocity of Electron in Bohr’s Orbit:

Now, ε_o, m, h, π, e are constant

∴ ω  ∝ 1 / n³

Thus the angular velocity of the electron in Bohr’s orbit of an atom is inversely proportional to the cube of the principal quantum number.

Notes:

• The frequency of electron in Bohr’s orbit of an atom is inversely proportional to the cube of the principal quantum number.
• The time period of the electron in Bohr’s orbit of an atom is directly proportional to the cube of the principal quantum number.
• The centripetal acceleration of electron in Bohr’s orbit of an atom is inversely proportional to the fourth power of the principal quantum number

The Expression for Energy of Electron in Bohr’s Orbit:

Let m be the mass of an electron revolving in a circular orbit of radius r with a constant speed v around the nucleus.  Let – e  and + e be the charges on the electron and the nucleus, respectively.

The  potential energy of electron having charge,  – e is given by

The total energy of the electron is given by

The total energy of electron  =  Kinetic energy of electron + Potential energy of the electron

This is the required expression for the energy of the electron in Bohr’s orbit of an atom. Since ε_o, m, h, π, e are constant

∴   E ∝  1 / n²

Thus the energy of an electron in Bohr’s orbit of an atom is inversely proportional to the square of the principal quantum number.

The negative sign indicates that the electron is bound to the nucleus by attractive force and to remove the electron from the atom energy must be supplied to the electron to overcome the attractive force. This energy is called the binding energy of the electron.

Merits of Bohr’s Model of Hydrogen Atom:

• This theory explains the spectrum of hydrogen atom completely.
• The concept of electronic configuration i.e. the distribution of electrons in different orbits was introduced.
• This theory is capable of explaining the line spectra of elements in general.
• This theory can be used to find the ionization potential of an electron in an atom.
• The value of Rydberg can be calculated using this theory.

Demerits of Bohr’s Model of Hydrogen Atom

• Though spectra of a simple atom like hydrogen is explained by Bohr’s Theory, it fails to account for elements containing
  more than one electron.
• A line in an emission spectrum splits up into a number of closely spaced lines when the atomic source of radiation is placed in
  the magnetic field. This is known as the Zeeman Effect. Bohr Theory could not explain this.
• A line in an emission spectrum splits up into a number of closely spaced lines when the atomic source of radiation is placed in an electric field, which is known as the Stark effect. Bohr Theory has no explanation for it.

Science > Physics > Atoms, Molecule, and Nuclei > Bohr’s Model of an Atom