Concept of Maximum Work

Science > Chemistry > Chemical Thermodynamics and Energetics > Concept of Maximum Work

According to the first law of thermodynamics, ΔU = q  +  W    In an isothermal process, ΔU  =   0, ∴   q   =   – W

Therefore, all the heat absorbed by the system is utilized to do work. (i.e. maximum utilization of the energy takes place. )

The work of expansion is given by the product of external pressure and the volume change. W = – P_ext ΔV

In any expansion, the external pressure must be less than the pressure of the gas. If the external pressure is zero, the work done is also zero as the gas expands into the vacuum. If the external pressure is increased gradually, more and more work will be done by the gas during expansion. If the external pressure becomes equal to the pressure of the gas, there will be no change in the volume and thus ΔV = 0. The work done is also zero. If P_ext is more than the pressure of the gas cannot expand. Therefore, when Pext becomes P then ΔV will be maximum. In the reversible process, P_ext is always less than the pressure of the gas, by an infinitesimally small quantity.

W =  (P –  dp) dV

In the equation W tends to the maximum as (P – dp) tends to P or dp tends to zero. Therefore work done in an isothermal reversible expansion of an ideal gas is maximum work.

Conditions for Maximum Work:

All the changes taking place in a system during the process are reversible. All the changes taking place in a system during the process should take place in infinitesimally small infinite steps. During the change, the driving and opposing forces should defer by an infinitesimally small amount. The system remains in mechanical equilibrium with the surroundings.

Expression for Maximum Work:

Work done in an isothermal reversible expansion is maximum work.

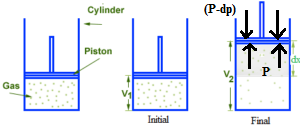
Consider  ‘n ‘ moles of an ideal gas enclosed in a cylinder fitted with a weightless, frictionless, airtight movable piston. Let the pressure of the gas be P which is equal to external atmospheric pressure P. Let the external pressure be reduced by an infinitesimally small amount dp and the corresponding small increase in volume be dV. So the small work done in the expansion process

dW  =  – P_ext . dV

∴ dW =  – (P  –  dp). dV

∴ dW =   – (P.dV  –  dp.dV)  …..  (1)

Since both dp and dV are very small, the product dp.dV is very small and can be neglected in comparison with P.dV. Then the above equation becomes

dW  =   – P.dV                ……….  (2)

When the expansion of the gas is carried out reversibly then there will be series of such p.dV terms. The total maximum work W_max can be obtained by integrating above equation between the limits V₁ to  V₂. Where V₁ is initial volume and V₂ is final volume.

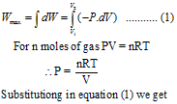
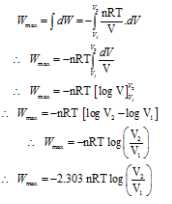
For an isothermal expansion, Boyle’s law is applicable.
Hence P₁V₁ = P₂V₂ i.e. V₂ / V₁ = P₁ / P₂

Where P₁  and P₂  are initial and final pressure respectively.

Notes:

• As the ratio of volumes or pressure is used in the above equation when work done is to be calculated the volumes and the pressures may be expressed in any unit, provided both the quantities are expressed in the same unit.
• The work obtained using the above equation will be in joule if R is taken in the S.I. unit.
• The number of moles  = Wt. in gram / Molecular wt.in grams
• Absolute temperature T k   = to C   + 273

Work is Path Function:

The work done in isothermal constant pressure process is given by

W   =    – Pext ΔV i.e. W   =    – Pext  ( V₂  –  V₁) 

Where, Pext = External opposing pressure

V₁ = Initial volume V₂ = Final volume.

The work done in the isothermal reversible process is given by

Where, n = Number of moles of the gas R = Universal gas constant

T = Absolute temperature of the gas

V₁ = Initial volume V₂ = Final volume

We can see that the work done depends on the manner or the conditions under which the process carried out. Thus it is not dependent on initial and final conditions of the system but on the path followed by the system. Hence work is path function or it is not a state function.

Numerical Problems on Maximum Work:

Example – 01:

3 moles of an ideal gas are expanded isothermally and reversibly from volume of 10 m³ to the volume 20 m³ at 300 K. Calculate the work done.

Given: n = 3 moles, V₁ = 10 m³, V₂ = 20 m³, T = 300 K, R = 8.314 J K^-1 mol^-1.

To Find: Work done =?

Solution:

Work done in isothermal reversible process is given by

W_max = -2.303 nRT log₁₀(V₂/V₁)

∴ W_max = -2.303 × 3 mol × 8.314 J K^-1 mol^-1 × 300 K × log₁₀( 20 m³/ 10 m³)

∴ W_max = -2.303 × 3 × 8.314 × 300 × log₁₀(2)

∴ W_max = -2.303 × 3 × 8.314 × 300 × 0.3010

∴ W_max = – 5187 J = – 5.187 kJ

Ans: maximum work done =  – 5187 J = – 5.187 kJ

Negative sign indicates the work is done by the system on the surroundings

Example – 02:

24 g of oxygen are expanded isothermally and reversibly from 1.6 × 10⁵ Pa pressure to 100 kPa at 298 K. Calculate the work done.

Given: m = 24 g, P₁ = 1.6 × 10⁵ Pa, P₂ = 100 kPa = 100 × 10³ Pa = 1 × 10⁵ Pa, T = 298 K, R = 8.314 J K^-1 mol^-1.

To Find: Work done =?

Solution:

Number of moles of oxygen = Given mass of oxygen / molecular mass of oxygen

Number of moles of oxygen = 24 g / 32 g mol^-1 = 0.75 mol

Work done in isothermal reversible process is given by

W_max =  -2.303 nRT log₁₀(P₁/P₂)

∴ W_max = -2.303 × 0.75 mol × 8.314 J K^-1 mol^-1 × 298 K × log₁₀( 1.6 × 10⁵ Pa / 1 × 10⁵ Pa)

∴ W_max = -2.303 × 0.75 × 8.314× 298 × log₁₀( 1.6)

∴ W_max = -2.303 × 0.75 × 8.314 × 298  × 0.2041

∴ W_max = – 873.4 J

Ans: maximum work done =  – 873.4 J

Negative sign indicates the work is done by the system on the surroundings

Example – 03:

4.4 × 10^-2 kg of CO₂ is compressed isothermally and reversibly at 293 K from the initial pressure of 150 kPa when work obtained is 1.245 kJ. Find the final pressure.

Given: m = 4.4 × 10^-2 kg, P₁ = 150 kPa, Maximum work of compression = W = + 1.245 kJ = 1245 J, T = 293 K, R = 8.314 J K^-1 mol^-1, P₂ =?

To Find: Final pressure =?

Solution:

Number of moles of CO₂ = Given mass of CO₂ / molecular mass of CO₂

Number of moles of CO₂ = n = 4.4 × 10^-2 kg / 44 × 10^-3 kg mol^-1 = 1 mol

Work done in isothermal reversible process is given by

W_max = -2.303 nRT log₁₀(P₁/P₂)

∴ 1245 J = -2.303 × 1 mol × 8.314 J K^-1 mol^-1 × 293 K × log₁₀(P₁/P₂)

∴ 1245 J = -2.303 × 1 mol × 8.314 J K^-1 mol^-1 × 293 K × log₁₀(P₂/P₁)

∴ log₁₀(P₂/P₁) = (1245) J / (2.303 × 1 × 8.314 × 293)  J

∴ log₁₀(P₂/P₁) = 0.2219

∴ (P₂/P₁) = Antilog (0.2219) = 1.667

∴ P₂ = 1.667 ×  P₁  = 1.667 × 150 kPa = 250 kPa

Ans: Final Pressure is 250 kPa

Example – 04:

2.8 × 10^-2 kg of nitrogen is expanded isothermally and reversibly at 300 K from the initial pressure of 15.15 × 10⁵ Nm^-2 when work obtained is 17.33 kJ. Find the final pressure.

Given: m = 42.8 × 10^-2 kg, P₁ = 15.15 × 10⁵ Nm^-2, Maximum work of expansion = W = – 17.33 kJ = – 17.33 × 10³ J, T = 293 K, R = 8.314 J K^-1 mol^-1, P₂ =?

To Find: Final Pressure =?

Solution:

Number of moles of Nitrogen = Given mass of Nitrogen / molecular mass of Nitrogen

Number of moles of Nitrogen = n = 2.8 × 10^-2 kg / 28 kg mol^-1 = 1 mol

Work done in isothermal reversible process is given by

W_max = -2.303 nRT log₁₀(P₁/P₂)

∴ – 17.33 × 10³ J = -2.303 × 1 mol × 8.314 J K^-1 mol^-1 × 300 K × log₁₀(P₁/P₂)

∴ 17.33 × 10³ J = 2.303 × 1 mol × 8.314 J K^-1 mol^-1 × 300 K × log₁₀(P₁/P₂)

∴ log₁₀(P₁/P₂) = (17.33 × 10³) J / (2.303 × 1 × 8.314 × 300)  J

∴  log₁₀(P₁/P₂) = 3.0170

∴ (P₁/P₂) = Antilog (3.0170) = 1040

∴ P₂ =  P₁ / 1040 = 15.15 × 10⁵ Nm^-2 / 1040 =  14056.7 Nm^-2

Ans: Final Pressure is 14056.7 Nm^-2

Example – 05:

3 moles of an ideal gas are compressed isothermally and reversibly at 22° C to a volume 2L when work done is 2.983 kJ. Find the initial volume.

Given: n = 3 mol, V₂ = 2 L, Maximum work of compression = W = + 2.983 kJ = 2.983 × 10³ J , T = 22° C = 22 + 273 = 295 K, R = 8.314 J K^-1 mol^-1, V₁ = ?,

To Find: Initial volume =?

Solution:

Work done in isothermal reversible process is given by

W_max =  -2.303 nRT log₁₀(V₂/V₁)

∴ 2.983 × 10³ J =  -2.303 ×3 mol × 8.314 J K^-1 mol^-1 × 295 K × log₁₀(V₂/V₁)

∴ 2.983 × 10³ J = 2.303 ×3 mol × 8.314 J K^-1 mol^-1 × 295 K × log₁₀(V₁/V₂)

∴ log₁₀(V₁/V₂) = 2.983 × 10³ J / (2.303 × 3 × 8.314 × 295)  J

∴ log₁₀(V₁/V₂) = 0.1760

∴ (V₁/V₂) = Antilog (0.1760) = 1.5

∴ V₁= 1.5  × V₂  = 1.5  ×  2 L  = 4 L

Ans: Initial Volume = 4 L

Example – 06:

280 mmol of an ideal gas occupy 12.7 L at 310 K. Calculate the work done when gas expands a) isothermally against constant external pressure 0.25 atm, b) isothermally and reversibly c) in a vacuum until its volume becomes 3.3 L.

Given: n = 280 mmoles = 0.280 mol, V₁ = 12.7 L, ΔV = 3.3 L, T = 310 K, R = 8.314 J K^-1 mol^-1. External Pressure = 0.25 atm

To Find: Work done =?

Solution:

a)  The gas expands isothermally against constant external pressure 0.25 atm

W = – P_ext × ΔV = – 0.25 atm × 3.3 L = – 0.825 L atm

W = – 0.825 L atm × 101.3  J L^-1 atm^-1 = – 83.6 J

Hence work done = – 83.6 J

Negative sign indicates the work is done by the system on the surroundings

b) Gas expands isothermally and reversibly

ΔV = (V₂ – V₁) = (V₂ –  12.7 L) =  3.3 L

V₂ = 3.3 L + 12.7 L = 16 L

Work done in isothermal reversible process is given by

W_max = -2.303 nRT log₁₀(V₂/V₁)

∴ W_max = -2.303 × 0.280 mol × 8.314 J K^-1 mol^-1 × 310 K × log₁₀( 16 L/ 12.7 L)

∴ W_max = -2.303 × 0.280 × 8.314 × 310 × log₁₀(1.260)

∴ W_max = -2.303 × 0.280 × 8.314 × 310 × 0.1004

∴ W_max = – 166.9  J

Maximum work = 166.9 J

Negative sign indicates the work is done by the system on the surroundings

c) Gas expands in vacuum

In this case, it is a free expansion, there is no opposing pressure. Hence P_ext = 0

W = – P_ext × ΔV = 0 atm × 3.3 L  = 0

Work done = 0

Example – 07:

 300 mmol of a perfect gas occupies 13 L at 320 K. Calculate the work done in joules when the gas expands a) isothermally against the constant external pressure of 0.20 atm. b) Isothermal and reversible process c) Into vacuum until the volume of the gas is increased by 3 L.

Given: n = 300 mmoles = 0.3 mol, V₁ = 13 L, ΔV = 3 L, T = 320 K, R = 8.314 J K^-1 mol^-1. External Pressure = 0.20 atm

To Find: Work done =?

Solution:

a)  The gas expands isothermally against constant external pressure 0.20 atm

W = – P_ext × ΔV = – 0.20 atm × 3 L = – 0.6 L atm

W = – 0.6 L atm × 101.3 J L^-1 atm^-1 = – 60.78 J

Hence work done = – 60.78 J

Negative sign indicates the work is done by the system on the surroundings

b) Gas expands isothermally and reversibly

ΔV = (V₂ –  V₁)  =  (V₂ –  13 L) =  3 L

V₂ = 3 L + 13 L = 16 L

Work done in isothermal reversible process is given by

W_max = -2.303 nRT log₁₀(V₂/V₁)

∴ W_max = -2.303 × 0.3 mol × 8.314 J K^-1 mol^-1 × 320 K × log₁₀( 16 L/ 13 L)

∴ W_max = -2.303 × 0.3 × 8.314 × 320 × log₁₀(1.231)

∴ W_max = -2.303 × 0.3 × 8.314 × 320 × 0.0902

∴ W_max = – 165.8  J

Maximum work = – 165.8  J

Negative sign indicates the work is done by the system on the surroundings

c) Gas expands in vacuum

In this case, it is the free expansion, there is no opposing pressure. Hence P_ext = 0

W = – P_ext × ΔV = 0 atm × 3 L  = 0

Work done = 0

Previous Topic: Pressure-Volume Type Work

Next Topic: First Law of Thermodynamics

Science > Chemistry > Chemical Thermodynamics and Energetics > Concept of Maximum Work