Work Done in Chemical Process

Science > Chemistry > Chemical Thermodynamics and Energetics > Work Done in Chemical Process

Pressure Volume Work:

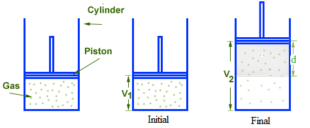
Consider an ideal gas having definite mass (say n moles) be enclosed in a cylinder fitted with weightless, frictionless, tightly fitted, movable piston. Let ‘A’ be the area of the cross-section of the cylinder. Let the gas expand from volume V₁ to V₂ against constant external pressure P_ext which is exerted on the piston. Due to expansion, the piston moves upward by a distance ‘d’. In this process, the system loses energy to the surroundings. Hence the work done by the system is negative.

Work done = – Opposing Force x displacement

∴   W = – F x displacement    …….  (1)

Now, pressure is force per unit area.

∴ Pressure   = Force /  Area

∴ Force = Pressure x  Area

∴       F        =      P   x    A   ……..  (2)

Substituting this value in equation (1)

∴   W   =     –  P   x   A    x   dx     ………. (3)

But,  A   x  dx  = Volume through gas expands

=   Change in volume =  ( V₂  –  V₁) = Δ V

Substituting this value in equation (3)

W = – P_ext ΔV

This is an expression for pressure volume work done in terms of pressure and volume in the isothermal expansion of an ideal gas against constant external pressure.

Notes:

• It is the external pressure against gas expands i.e. P_ext and not the pressure of the gas that is used in evaluating the pressure volume work done.
• The final equation shows that work  W  depends only on the change in volume (ΔV) and opposing pressure (P_ext) and not on the quantity of the gas (i.e. it is independent of the number of moles) and Temperature of the gas (T).
• The work done by the system in a process depends on the way or manner in which it is carried out. Work, therefore, is not a state function. It is a path function.

Free Expansion:

The free expansion is also known as work of expansion in a vacuum. When a gas expands in a vacuum there is no opposing force i.e.  P_ext = 0.

For getting work done opposing force is necessary, hence no work is done when a gas expands in a vacuum. Such an expansion is called as free expansion.

W   =    – P_ext ΔV

∴ W   =  0 × ΔV = 0

Work Done in a Cyclic Process:

A cyclic process is one which consists of a series of intermediate steps, at the end of which the system returns to its initial state.

Since in a cycle, initial and final states are the same.

∴ Δ(state function)   =   0

∴ ΔU =  0 (i.e. No change in internal energy)

Now,   ΔU   = q + W

∴ 0 = q  +   W

∴ q = -W

Thus in a cyclic process heat absorbed by the system from the surrounding (q) is equal to work done (W) by the system on the surrounding.

Difference Between Heat and Work: 

When heat is added to gas the random motion of molecules of gas increases, thus heat is a stimulus to gas which increases the random motion of the gas molecules. Thus heat is a random form of energy. Now let us consider work done on a system by compressing the gas in a cylinder. The movement of the piston makes the gas molecules to move in the direction of applied force. Thus work is a stimulus which increases the organized motion of the molecules of the gas. Thus work is an organized form of energy.

Sign Convention Used in Thermodynamics:

• During the expansion, V₂ > V₁, Hence ΔV is positive.    Hence work done W is negative. Thus when the work is done by the system on the surrounding i.e. Work of expansion is taken as negative (- W).
• During compression, V₂ < V₁, Hence ΔV is negative. Hence work done W is positive. Thus when the work done on the system by the surrounding i.e. Work of compression is taken as positive (+W).

Numerical Problems on Pressure Volume Work:

Example – 01:

2 moles of an ideal gas are expanded isothermally from volume of 15.5 L to the volume 20 L against a constant external pressure of 1 atm. Calculate the pressure-volume work in L atm and J.

Given: n = 2 moles, V₁ = 15.5 L, V₂ = 20 L, P_ext = 1 atm

To Find: Work Done =?

Solution:

Work done in an isothermal process is given by   W = – P_ext × ΔV

∴ W = – P_ext × (V₂ – V₁) = – 1 atm × (20 L – 15.5 L)

∴ W = – 1 atm × (4.5 L) = – 4.5 L atm

W = – 4.5 L atm × 101.3 J L^-1 atm^-1 = – 455.8 J

Ans: work done = – 4.5 L atm or – 455.8 J

The negative sign indicates the work is done by the system on the surroundings

Example – 02:

2 moles of an ideal gas are compressed isothermally from volume of 10 dm³ to the volume 2 dm³ against a constant external pressure of 1.01 × 10⁵ Nm^-2. Calculate the pressure-volume work done.

Given: n = 2 moles, V₁ = 10 dm³ = 10 × 10^-3 m³, V₂ = 2 dm³ = 2 × 10^-3 m³, P_ext = 1 atm.

To Find: Work Done =?

Solution:

Work done in an isothermal process is given by   W = – P_ext × ΔV

∴ W = – P_ext × (V₂ – V₁) = – 1.01 × 10⁵ Nm^-2 × (2 × 10^-3 m³ – 10 × 10^-3 m³)

∴ W = – P_ext × (V₂ – V₁) = – 1.01 × 10⁵ Nm^-2 × (- 8 × 10^-3 m³)

∴ W = + 8.08 × 10² J = + 808 J

Ans: work done = + 808 J

Positive sign indicates the work is done by the surrounding on the system

Example – 03:

3 moles of an ideal gas are expanded isothermally from volume of 300 cm³ to the volume 2.5 L against a constant external pressure of 1.9 atm at 300 K. Calculate the pressure volume work in L atm and J.

Given: n = 3 moles, V₁ = 300 cm³= 0.3 L, V₂ = 2.5 L, P_ext = 1.9 atm

To Find: Work Done =?

Solution:

Work done in an isothermal process is given by   W = – P_ext × ΔV

∴ W = – P_ext × (V₂ – V₁) = – 1.9 atm × (2.5 L – 0.3 L)

∴ W = – 1.9 atm × (2.2 L) = – 4.18 L atm

W = – 4.18 L atm × 101.3 J L^-1 atm^-1 = – 423.4 J

Ans: work done = – 4.5 L atm or – 423.4 J

The negative sign indicates the work is done by the system on the surroundings

Example – 04:

1 mole of an ideal gas is compressed isothermally from a volume of 500 cm³ against a constant external pressure of 1.216 × 10⁵ Pa. The pressure-volume work involved in the process is 36.5 J. calculate the final volume.

Given: n = 1 mole, V₁ = 500 cm³= 500 × 10^-6 m³, P_ext = 1.216 × 10⁵ Pa = = 1.216 × 10⁵ Nm^-2, Work of compression = + 36. 5 J, V₂ =?

To Find: Final volume = V₂ =?

Solution:

Work done in isothermal process is given by W = – P_ext × ΔV

∴ W = – P_ext × (V₂ – V₁)

∴ 36.5 J= – 1.216 × 10⁵ Nm^-2 × (V₂ – 500 × 10^-6 m³)

∴ 36.5 J/ 1.216 × 10⁵ Nm^-2 = – (V₂ – 500 × 10^-6 m³)

∴300 × 10^-6 m³ = (500 × 10^-6 m³ – V₂)

∴    V₂    = (500 × 10^-6 m³ – 300 × 10^-6 m³)

∴    V₂    = 200 × 10^-6 m³ = 200 cm³

Ans: final volume = 200 cm³

Example – 05:

1 mole of an ideal gas is compressed isothermally from volume of 20 L to 8 L against constant external pressure, when pressure volume work obtained is 44.9 L atm. Find the constant external pressure.

Given: n = 1 mol, V₁ = 20 L, V₂ = 8 L, Work of compression W = + 44.9 L atm, P_ext =?

To Find: External pressure =?

Solution:

Work done in isothermal process is given by   W = – P_ext × ΔV

∴ W = – P_ext × (V₂ – V₁)

∴ 44.9 L atm = – P_ext × (8 L – 20 L)

∴ 44.9 L atm = – P_ext × (- 12 L)

∴ P_ext   =44.9 L atm / 12 L)

∴ P_ext   = 3.74 atm

Ans: constant external pressure is 3.74 atm

Example – 06:

One mole of a gas expands by 3 L against a constant pressure of 3 atmosphere. Calculate the pressure volume work done in a) L-atm b) joules and c) calories.

Given: n = 1 mole, Δ V = 3 L, P_ext = 3 atm

To Find: Work Done =?

Solution:

Work done in isothermal process is given by   W = – P_ext × ΔV

∴ W = – 3 atm × 3 L = – 9 L atm

∴ W = – 9 L atm × 101.3 J L^-1 atm^-1 = – 911.7 J

∴ W = – 911.7 J / 4.184 J cal^-1 = – 217.9 cal

Ans: work done = – 9 L atm or – 911.7 J  or -217.9 cal

Negative sign indicates the work is done by the system on the surroundings

Example – 07:

100 mL of ethylene(g) and 100 mL of HCl (g) are allowed to react at  2 atm pressure as per the reaction given below. Calculate pressure volume type of work in it in joules.

C₂H_4(g)    +  HCl_(g)    →     C₂H₅Cl_(g)

Solution: 

Given: P_ext = 2 atm and the given reaction is

C₂H_4(g)    +  HCl_(g)    →     C₂H₅Cl_(g)

1 Vol               1Vol                      1Vol

100 mL            100 mL                  100 mL

Thus 100 ml of C₂H_4(g) reacts with 100 mL of HCl_(g)  to give 100 mL of C₂H₅Cl_(g).

Initial volume = Volume of reactants = 100 mL + 100 mL = 200 mL = 0.2 L

Final volume = Volume of products = 100 mL = 0.1 L

Work done in isothermal process is given by   W = – P_ext × ΔV

∴ W = – P_ext × (V₂ – V₁) = – 2 atm × (0.1 L – 0.2 L)

∴ W = – 2 atm × (- 0.1 L) = 0.2  L atm

W = 0.2 L atm × 101.3 J L^-1 atm^-1 = 20.26 J

Ans: work done = + 20.26 J

Positive sign indicates the work is done by the surroundings on the system

Example – 08:

A gas cylinder of 5 L capacity containing 4 kg of helium gas at 27 °C developed a leakage leading to the escape of the gas into atmosphere. If atmospheric pressure is 1.0 atm. calculate the pressure volume work done by the gas assuming ideal behaviour.

Given: V₁ = 5 L, mass of gas m = 4 kg = 4 × 10³ g, T = 27 °C = 27 +273 = 300 K,  P_ext = P = 1.0 atm, R = 0.0821 L atm K^-1 mol^-1.

To Find: Work Done =?

Solution:

Number of moles = Given mass of He / Molecular mass of He = 4 × 10³ g / 4 g = 10³

By ideal gas equation, we have P V₂ = nRT

∴   V₂ = nRT / P = 10³ × 0.0821 × 300 / 1   = 2.463 × 10⁴ L = 24630 L

Work done in isothermal process is given by   W = – P_ext × ΔV

∴ W = – P_ext × (V₂ – V₁) = – 1 atm × (24630 L – 5 L)

∴ W = – 1 atm × (24625 L) = – 24625 L atm

W = – 24625 L atm × 101.3 J L^-1 atm^-1 = – 2.494 × 10⁶ J = – 2494 kJ

Ans: work done = – 2494 kJ

Negative sign indicates the work is done by the system on the surroundings

Example – 09:

1.6 mol of water evaporates at 373 K against atmospheric pressure of 1 atm. Assuming ideal behaviour of water vapours calculate the work done.

Given: n = 1.6 mole, T = 373 K, P_ext = P = 1.0 atm, R = 0.0821 L atm K^-1 mol^-1.

To Find: Work Done =?

Solution:

The molecular mass of water 18 g. and the density of water is 1 g per cc

Hence initial volume of water = V₁ = 18 x 1.6 x 10^-3 L = 0.0288 L

By ideal gas equation, we have P V₂ = nRT

∴   V₂ = nRT / P = 1.6 × 0.0821 × 373 / 1   = 48.93 L

Work done in isothermal process is given by   W = – P_ext × ΔV

∴ W = – P_ext × (V₂ – V₁) = – 1 atm × (48.93 L – 0.0288 L)

∴ W = – 1 atm × (48.90 L) = – 48.90  L atm

W = – 48.90 L atm × 101.3 J L^-1 atm^-1 = – 4954.8 J

Hence work done = – 4954.8 J

Negative sign indicates the work is done by the system on the surroundings

Example – 10:

1.0 mol of water evaporates at 373 K against atmospheric pressure of 749.8 mm of Hg. Assuming ideal behaviour of water vapours calculate the pressure volume work done.

Given: n = 1.0 mole, T = 373 K, P_ext = P = 749.8 mm of H = 749.8 / 760 = 0.987 atm, R = 0.0821 L atm K^-1 mol^-1.

To Find: Work Done =?

Solution:

The molecular mass of water 18 g. and the density of water is 1 g per cc

Hence initial volume of water = V₁ = 18 x 1.0 x 10^-3 L = 0.018 L

By ideal gas equation, we have P V₂ = nRT

∴   V₂ = nRT / P = 1.0 × 0.0821 × 373 / 0.987   = 31.03 L

Work done in isothermal process is given by   W = – P_ext × ΔV

∴ W = – P_ext × (V₂ – V₁) = – 0.987 atm × (31.03 L – 0.018 L)

∴ W =  –  0.987 atm × (31.01 L) = – 30.61  L atm

W = – 30.61 L atm × 101.3 J L^-1 atm^-1 = – 3101 J

Ans: work done = – 3101 J

Negative sign indicates the work is done by the system on the surroundings

Previous Topic: Concept of Internal Energy

Next Topic: Concept of Maximum Work

Science > Chemistry > Chemical Thermodynamics and Energetics > Work Done in Chemical Process